Во многих задачах, связанных с прямыми в пространстве, необходимо выяснить взаимное расположение двух прямых. Это удобно осуществлять используя направляющие векторы прямых. Если направляющие векторы 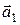 и
и 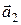 прямых L
прямых L 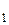 и L
и L  коллинеарны, то прямые L
коллинеарны, то прямые L 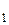 и L
и L 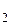 совпадают или параллельны. Далее наличие или отсутствие общей точки у прямых L
совпадают или параллельны. Далее наличие или отсутствие общей точки у прямых L 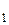 и L
и L  покажет, совпадают они или параллельны. Если же направляющие векторы
покажет, совпадают они или параллельны. Если же направляющие векторы  и
и 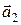 неколлинеарны, то это равносильно тому, что прямые L
неколлинеарны, то это равносильно тому, что прямые L 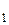 и L
и L 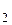 пересекаются или скрещиваются. В первом случае прямые L
пересекаются или скрещиваются. В первом случае прямые L 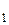 и L
и L 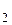 имеют одну общую точку, а во втором случае общих точек они не имеют. В ситуациях, когда прямые параллельны или скрещиваются, можно говорить о расстоянии между этими прямыми. Напомним, что расстоянием между скрещивающимися прямыми L
имеют одну общую точку, а во втором случае общих точек они не имеют. В ситуациях, когда прямые параллельны или скрещиваются, можно говорить о расстоянии между этими прямыми. Напомним, что расстоянием между скрещивающимися прямыми L  и L
и L  называется наименьшее из расстояний между различными точками
называется наименьшее из расстояний между различными точками 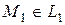 и
и  .
.
Рассмотрим также проблему взаимного расположения прямой и плоскости в пространстве. Для того, чтобы выяснить взаимное расположение прямой L и плоскости П, проще всего воспользоваться направляющим вектором прямой L и нормальным вектором  плоскости П. Если векторы
плоскости П. Если векторы  и
и 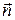 не ортогональны, то это равносильно тому, что L и П пересекаются в единственной точке. Если же векторы
не ортогональны, то это равносильно тому, что L и П пересекаются в единственной точке. Если же векторы 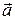 и
и 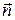 ортогональны, то это равносильно тому, что прямая L параллельна плоскости П или лежит в ней.
ортогональны, то это равносильно тому, что прямая L параллельна плоскости П или лежит в ней.
6.2.1 Пример. Заданы прямые:
L 1: 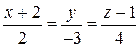 и L 2:
и L 2:  .
.
При каком значении a они пересекаются?
 Решение. Обозначим через
Решение. Обозначим через 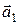 и
и 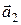 направляющие векторы прямых L
направляющие векторы прямых L 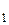 и L
и L  ;
;  ,
, 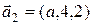 . Прямые L
. Прямые L  и L
и L  пересекаются тогда и только тогда, когда векторы
пересекаются тогда и только тогда, когда векторы  и
и 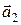 неколлинеарны, а векторы
неколлинеарны, а векторы 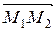 ,
, 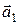 ,
, 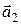 компланарны, где
компланарны, где 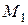 − точка прямой L
− точка прямой L 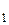 ,
, 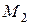 − точка прямой L
− точка прямой L  . Возьмем
. Возьмем  ,
,  (рисунок 9). Ясно, что векторы
(рисунок 9). Ясно, что векторы 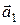 и
и 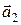 неколлинеарны, т.к.
неколлинеарны, т.к. 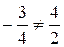 . Находим координаты вектора
. Находим координаты вектора 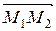
 Вычисляем смешанное произведение векторов
Вычисляем смешанное произведение векторов 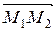 ,
,  ,
, 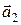 :
:

Для компланарности векторов 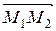 ,
, 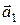 ,
, 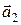 необходимо и достаточно, чтобы
необходимо и достаточно, чтобы 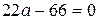 , т.е.
, т.е. 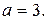 Итак, при
Итак, при 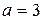 прямые L
прямые L  и L
и L 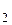 пересекаются. При других значениях
пересекаются. При других значениях 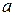 прямые L
прямые L  и L
и L 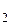 не пересекаются и не параллельны, т.е. скрещиваются.
не пересекаются и не параллельны, т.е. скрещиваются.
6.2.2 Пример. Заданы две прямые:
L 1: 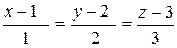 и L 2:
и L 2:  .
.
Доказать, что прямые L  и L
и L  скрещиваются, и найти расстояние между ними.
скрещиваются, и найти расстояние между ними.
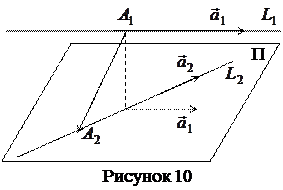 Решение. Выпишем направляющие векторы прямых L
Решение. Выпишем направляющие векторы прямых L  и L
и L  :
: 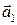 =(1,2,3),
=(1,2,3), 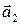 =(1,−1,1). Векторы
=(1,−1,1). Векторы  и
и 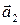 неколлинеарны, поэтому
неколлинеарны, поэтому 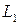 и
и 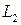 пересекаются или скрещиваются. Покажем, что пересечения нет. Для этого достаточно показать, что
пересекаются или скрещиваются. Покажем, что пересечения нет. Для этого достаточно показать, что  и
и  не лежат в одной плоскости. С этой целью построим плоскость П, проходящую через L
не лежат в одной плоскости. С этой целью построим плоскость П, проходящую через L  и параллельную прямой L
и параллельную прямой L  (рисунок 10). Плоскость П поможет нам в нахождении расстояния между
(рисунок 10). Плоскость П поможет нам в нахождении расстояния между 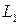 и
и 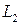 . Выберем произвольно две точки на прямых
. Выберем произвольно две точки на прямых  и
и 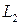 , например A
, например A  (1,2,3)
(1,2,3) 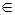 L
L  ; A
; A  (1, −1, −4)
(1, −1, −4) 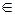 L
L  . Искомая плоскость П проходит через точку A
. Искомая плоскость П проходит через точку A  параллельно векторам
параллельно векторам 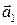 и
и 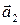 , поэтому её уравнение имеет вид:
, поэтому её уравнение имеет вид:
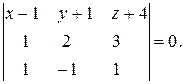
Отсюда получаем П: 5 x +2 y −3 z −15=0. Очевидно, что A 
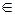 П, поэтому L
П, поэтому L 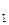
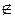 П, значит прямые L
П, значит прямые L  и L
и L  скрещиваются. Искомое расстояние между L
скрещиваются. Искомое расстояние между L  и L
и L  равно расстоянию от A
равно расстоянию от A  до плоскости П (см. рисунок 10). Расстояние d от точки А до плоскости П вычисляем по следующей формуле:
до плоскости П (см. рисунок 10). Расстояние d от точки А до плоскости П вычисляем по следующей формуле:
 , где
, где 
Получаем
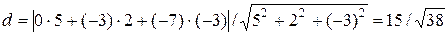 .
.
Упражнения
6.3.1 Записать канонические уравнения прямой, проходящей через точку М(1,0,−1) параллельно вектору 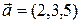 .
.
6.3.2 Записать параметрические уравнения прямой, проходящей через точку М(1, −1, −3) параллельно вектору 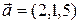 .
.
6.3.3 Записать канонические уравнения прямой, заданной общими уравнениями
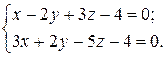
6.3.4 Заданы две прямые:
L  :
: 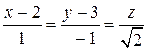 и L
и L  :
: 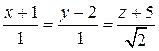 .
.
Выяснить их взаимное расположение.
6.3.5 Заданы две прямые:
L  :
: 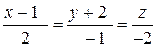 и L
и L  :
: 
Доказать, что прямые пересекаются, и найти точку их пересечения.
6.3.6 Заданы две прямые:
L  :
:  L
L 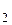 :
: 
Показать, что прямые L  и L
и L 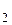 перпендикулярны.
перпендикулярны.
6.3.7 Написать уравнение плоскости, проходящей через прямую  и точку
и точку 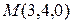 .
.
6.3.8 Найти ортогональную проекцию точки 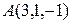 на плоскость x +2 y +3 z +8=0.
на плоскость x +2 y +3 z +8=0.
6.3.9 Найти ортогональную проекцию прямой 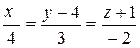 на плоскость x +2 y +4 z −7=0.
на плоскость x +2 y +4 z −7=0.
6.3.10 Написать уравнение плоскости, проходящей через ось Oz и составляющей с плоскостью 2 x + y − 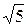 z =0 угол
z =0 угол 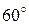 .
.
6.3.11 Заданы две прямые:
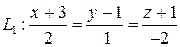 и
и 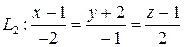 .
.
Доказать, что прямые  и
и 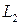 параллельны и найти расстояние между ними.
параллельны и найти расстояние между ними.
6.3.12 Заданы две прямые:
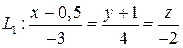 и
и 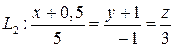 .
.
Доказать, что прямые L  и L
и L 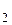 скрещиваются, и найти расстояние между ними.
скрещиваются, и найти расстояние между ними.
Контрольные задания
Рекомендуемая литература [1, гл. 2, §2−3], [2, гл. 5, §5.8, 5.9, 5.12, 5.18].
6.4.1 Написать канонические уравнения прямой, проходящей через точку A(1,2, −2) и параллельной прямой 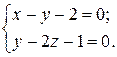
6.4.2 Задана прямая и плоскость:
 6 x −3 y +2 z =0.
6 x −3 y +2 z =0.
Найти точку их пересечения и угол между ними.
6.4.3 Заданы две прямые:
 и
и 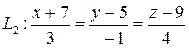 .
.
Доказать, что прямые 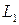 и
и 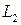 параллельны и найти расстояние между ними.
параллельны и найти расстояние между ними.
6.4.4 Заданы две прямые:
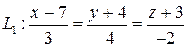 и
и 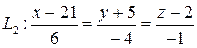 .
.
Доказать, что прямые L  и L
и L  скрещиваются и найти расстояние между ними.
скрещиваются и найти расстояние между ними.
Список литературы
1 Курс аналитической геометрии и линейной алгебры / Д. В. Беклемишев. – М.: Наука, 1976.
2 Основы линейной алгебры и аналитической геометрии / Е. И. Гурский. – Минск: Выш. шк., 1982.
3 Высшая математика. Ч. I. / Р. М. Жевняк, А. А. Карпук. – Минск: Выш. шк., 1984.
 2020-10-12
2020-10-12 251
251







