Умножение вектора на число

Пусть дано вектор 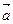 и чис­ло р. Произведением вектора  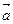на число р называется новый вектор 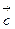, коллинеарный векто­ру 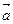, имеющий длину

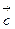 | | = | р || 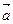| и то же самое направление, что и вектор 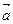, если р>0, и

противоположное направление, если р 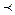О,  при этом  = р 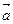 = 0, если р = 0 или  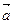= 0.                   

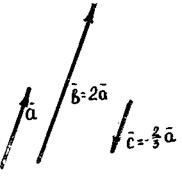
На рис. вектор 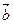 = 2 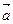 (число р = 2), а вектор  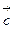=-  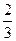а (число р = - ).

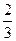Противоположный вектор – 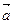 можно рассматривать как результат умножения вектора  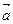на р = -1:   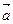    -  = (-1) .

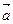Так, западный ветер можно представить как отрицательный восточный ветер.

Очевидно, что 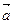 + (- ) = 0.

Из определения произведения вектора на число следует свойство этого произведения:

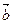 = p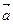

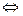
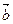
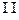
Сложение двух скользящих векторов определено лишь в случае, когда прямые, на которых они расположены, пересекаются. Тогда каждый из векторов переносится вдоль своей прямой в точку пересечения этих прямых, после чего сложение осуществляется по правилу параллелограмма.

Сложение двух фиксированных векторов определено лишь в случае, когда они имеют общее начало. Их сложение в этом случае осуществляется по правилу параллелограмма.