Правая и левая системы трех направлений

Рассмотрим три орта 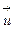, , 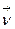, 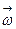не параллельных одной и той же плоскости, и вообразим, что их начала совмещены.

Представим себе наблюдателя, расположенного вдоль орта  так, что этот орт направлен от ног наблюдателя к голове, и вообразим, что наблюдатель смотрит по направлению орта 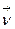. Тогда могут представиться два случая [1]): либо (рис. а) - орт  направлен (по отношению к наблюдателю) слева направо, либо (рис. b) —справа налево. В первом случае направления 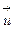, , 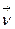 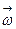(взятые в указанном порядке) составляют левую систему, а во втором — правую. Название «левая» происходит от того, что в первом случае орты 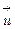, , 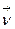 (взятые в указанном порядке) ориен­тированы друг относительно друга так, как большой, указатель­ный и средний пальцы левой руки (предполагается, что первые два пальца вытянуты, а третий согнут под углом к ладони). Таким же образом орты 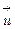, , 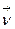, 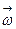составляющие правую систему, связаны с пальцами правой руки.

Левая система ортов 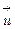, , 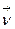останется левой, если произвести «круговую перестановку» (круговой перестановкой нескольких элементов а, b, с,..., k, рас­положенных в определенном порядке, называется такая перестановка, при которой каждый элемент заменяется на следующий, а последний — на пер­вый. Например, применяя круговую перестановку к трем элементам а, b, с, получим b, с, а. Производя круговую перестановку еще раз, получим с, а, b. Если произведем круговую перестановку еще раз, то вернемся к старому порядку) их, т. е. рассматривать их в порядке 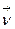, , Аналогичное свойство имеет место для правой системы. Наоборот, левая система перейдет в правую и обратно, если поме­нять местами только два орта. Например, если система 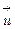, , 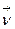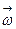левая, то система , ,  будет правой. Зеркальное отражение левой системы даёт правую, и обратно.

Так же можно различать левую и правую системы трех векто­ров, трех осей и вообще трех направлений.

Во многих вопросах геометрии и прикладной математики, кроме рассмотренного уже нами скалярного произведения, играет большую роль понятие так называемого векторного произведе­ния двух векторов, к определению которого мы переходим.

Векторным произведением векторов 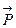 и 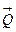 называ­ется вектор , определяемый следующими условиями:

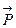a)    длина вектора  численно равна произведению длин векторов  и 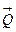 и синуса угла , заключенного между ними:          

Иными словами, длина вектора  численно равна площади параллелограмма, построенного на векторах 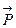 и 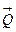 (в предположении, что эти векторы проведены из общего начала), или, что все равно,— удвоенной площади треуголь­ника, построенного на этих векторах (рис.).

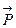b)    вектор  перпендикулярен к плоскости векторов  и 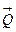, то есть к плоскости, параллельной векторам  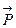и 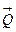. Можно для наглядности представить себе, что начала этих векторов совмещены, как на рис., тогда упомянутая плоскость есть плоскость, содержащая векторы  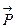и 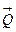 (или всякая ей параллельная).

Эти условия еще не вполне определяют вектор : остается сде­лать выбор между двумя возможными противоположными направ­лениями. Чтобы устранить эту двойственность, мы добавляем следующее условие:

c)    векторы 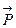, , 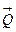 (в указанном порядке) составляют левую систему.