Упражнения и дополнения

1. Векторный момент относительно точки. Пусть 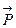 =  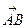— некоторый связанный или скользящий вектор и пусть С — некоторая точка. Векторным моментом вектора  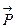относительно точки С называют вектор 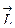, приложенный к точке С и определяемый следующими условиями: длина вектора  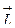численно равна произведению длины вектора  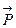и перпендикуляра h, опущенного из точки С на прямую, содержащую век­тор 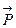; вектор  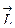перпендикулярен к плоскости CAB и направлен в такую сторону, чтобы векторы 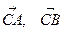,  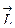составляли левую систему.

Точка С называется центром (или полюсом) момента.

Легко видеть, что момент вектора относительно данной точки не изме­нится, если переместить этот вектор вдоль прямой, содержащей его. Наобо­рот, если перемещать эту прямую, то момент будет изменяться, так как при этом будет изменяться либо величина h, либо направление 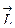, либо и то, и другое вместе. Вот почему понятие момента применяют только к скользя­щим или связанным векторам, но не к свободным, которые можно произ­вольно перемещать (не изменяя направления).

Предлагается доказать, что =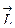

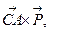
2.    Предлагается доказать:  Mомент равнодействующей нескольких векторов, приложенных к данной точке А, равен сумме моментов составляющих («обобщенная теорема Вариньона»).

О размерности. В приложениях математики часто рассматриваются величины, изображаемые векторами: силы, скорости, моменты сил и т. д. Векторам, изображающим такие величины, приписывается размерность. Не вдаваясь в существо дела, мы ограничимся изложением формальных правил действий с размер­ностями. С формальной точки зрения размерность — это одно­член, составленный из какого-то набора символов. Такие одночлены перемножаются и делятся по обычным прави­лам действий над одночленами. Имеют место следующие правила действий с размерностями:

Складывать векторные величины можно только в том случае, когда их размерности совпадают. При этом размерность суммы та же, что и у слагаемых.

При умножении векторной величины на скалярную их размерности перемножаются.

Модуль векторной величины имеет ту же размер­ность, что и сама величина.

Скалярное и векторное произведение имеют размер­ность, равную произведению размерностей сомножителей. Это легко следует из их определений и предыдущего правила.

Для того чтобы изобразить векторную величину на чертеже, мы должны условиться о масштабе: сколькими единицами длины мы будем изображать одну единицу данной размерности (например, км, м/сек, И).

Если в векторном произведении сомножители имеют размерность длины, то произведение имеет размерность площади. Масштаб для изображения единиц площади выбирается так, чтобы одна единица площади изобража­лась одной линейной единицей. При этом длина вектор­ного произведения будет численно равна площади парал­лелограмма, построенного на сомножителях.

Поскольку единица длины у нас выбрана раз навсегда и не меняется, указанное соглашение ни к каким проти­воречиям привести не может. Однако оно не так безобид­но, как может показаться. Именно, два математика поль­зующиеся этим соглашением, но разными единицами длины (например, француз, пользующийся сантиметрами, и англичанин — дюймами), для одних и тех же векторов нарисуют несовпадающие векторные произведения.