Якщо відомі координати векторів 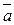 та
та 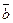 , то
, то
 (1.5)
(1.5)
Приклад 1. Обчислити 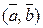 , якщо
, якщо  .
.
Розв’язання:
Користуючись формулою (1.4) знаходимо
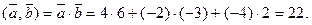
Відповідь: 
Приклад 2. При якому значенні m вектори  будуть перпендикулярними?
будуть перпендикулярними?
Розв’язання:
Два вектори перпендикулярні, якщо скалярний добуток дорівнює нулеві, тобто користуючись формулою (1.4) знаходимо скалярний добуток векторів 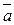 та
та 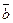 , тобто
, тобто  Оскільки вектори
Оскільки вектори 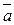 та
та 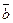 перпендикулярні, то
перпендикулярні, то  Отже,
Отже,  Звідси отримаємо, що
Звідси отримаємо, що 
Відповідь: При  вектори
вектори 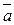 та
та 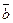 перпендикулярні.
перпендикулярні.
Приклад 3. Обчислити роботу, яка виконує сила  , коли її точка прикладання рухається прямолінійно, переміщуючись із положення А(2; -3; 5) в положення В(3; -2; -1).
, коли її точка прикладання рухається прямолінійно, переміщуючись із положення А(2; -3; 5) в положення В(3; -2; -1).
Розв’язання:
Згідно з формулою (1.3) робота  . Вектор переміщення
. Вектор переміщення  .
.
Тоді  Отже, робота А, яку виконує сила
Отже, робота А, яку виконує сила  , дорівнює 31.
, дорівнює 31.
Відповідь: робота А дорівнює 31.
Приклад 4. Дано вершини ΔАВС А(-1; 2; 4), В(-4; -2; 0), С(3; -2; 1). Знайти його внутрішній кут при вершині В.
Розв’язання:
Кут φ – це кут між векторами 
 Тоді використовуючи формулу (1.5) отримаємо:
Тоді використовуючи формулу (1.5) отримаємо:

Отже, φ=450.
Відповідь: Кут при вершині В дорівнює 450.
Приклад 5. Дано вектори  Знайти проекцію вектора
Знайти проекцію вектора  .
.
Розв’язання:
Користуючись формулою (1.2) знаходимо
 .
.
Далі знаходимо скалярний добуток векторів  .
.


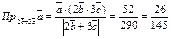 .
.
Відповідь: Проекція вектора  дорівнює
дорівнює 
Векторний добуток і його властивості.
Означення 2. Векторним добутком векторів 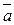 та
та 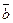 називається
називається  , який задовольняє умовам:
, який задовольняє умовам:
1) вектор  перпендикулярний до векторів
перпендикулярний до векторів 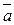 та
та 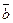 ;
;
2) довжина  вектора
вектора  дорівнює площі паралелограма побудованого на векторах
дорівнює площі паралелограма побудованого на векторах 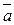 та
та 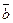 ;
;
3) якщо звести вектори  та
та 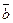 та
та  до спільного початку, то спостерігач, який міститься в кінці вектора
до спільного початку, то спостерігач, який міститься в кінці вектора  бачитиме найкоротший поворот від вектора
бачитиме найкоротший поворот від вектора  до вектора
до вектора 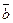 , таким, що відбувається проти годинникової стрілки
, таким, що відбувається проти годинникової стрілки
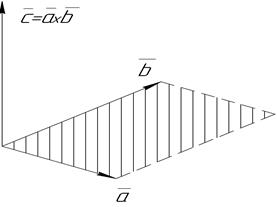
Рис. 11
 2020-10-12
2020-10-12 142
142








