Векторний добуток і його властивості

Означення 14. Три вектори називаються впорядкованою трійкою (або просто трійкою), якщо вказано, який з цих векторів являється першим, який – другим, і який – третій.

Означення 15. Трійка некомпланарних векторів 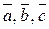 називається правою (лівою), якщо виконується одна із наступних трьох умов:

1. якщо, вектори зведені до спільного початку, і вони розміщені так, що можуть бути розташовані відповідно великий, не зігнутий вказівний і середній пальці правої (лівої) руки;

2. якщо після зведення до спільного початку вектор 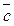 розташований по ту сторону від площини, яка визначається векторами 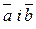, звідки найкоротший поворот від  до 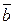 здійснюється проти часової стрілки (за часовою стрілкою);

3. якщо знаходячись всередині внутрішнього кута, утвореного приведеним до спільного початку векторів 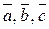, ми бачимо поворот від  до 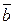і від нього до  здійснюється проти часової стрілки (за часовою стрілкою)

Означення 16. Афінна або Декартові система координат називається правою (лівою), якщо три базисних вектора утворюють праву(ліву) трійку

Означення 17. Векторним добутком векторів  та 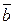називається 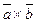, який задовольняє умовам:

1) вектор  перпендикулярний до векторів  і ;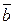

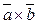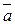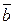
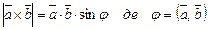2) довжина ׀ ׀ вектора  дорівнює площі паралелограма побудованого на векторах  і                           (23)

Рис.8

Основні властивості векторного добутку

1. 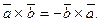  (векторний добуток залежить від послідовності співмножників)

2.

3.

4. векторний добуток дорівнює нульовому вектору тоді і тільки тоді, коли вектори колінеарні (паралельні) або хоча б один з них нульовий тобто .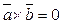

Формула вираження векторного добутку через координати співмножників має вигляд:

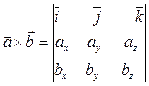                                       (24)

Приклад 14. Дано точки А(2; -1; 2), В(1; 2; -1), С(3; 2; 1). Знайти векторний добуток векторів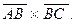

Розв’язання:

Знаходимо координати векторів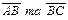

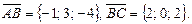
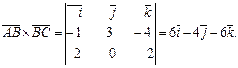
Отже,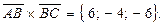

Відповідь: Векторний добуток векторів 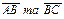дорівнює