Y = {y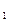 , y
, y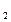 , …, y
, …, y } — множество исходов эксперимента, y
} — множество исходов эксперимента, y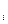 — i-ый исход эксперимента. Каждый из y
— i-ый исход эксперимента. Каждый из y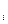 связан с соответствующим элементом состояния природы.
связан с соответствующим элементом состояния природы.
Z = {z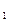 , z
, z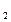 ,…, z
,…, z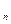 } — множество состояний природы. В общем случае статистическая связь:
} — множество состояний природы. В общем случае статистическая связь:
P(y/z) — условная вероятность исхода y при данном состоянии природы z.
P(y/z)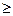 0;
0; 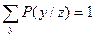 ,
, 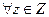 .
.
Совокупность из трёх элементов пространства Z, Y с заданными на Y условными вероятностями называют пространством выборок.
V = {x, y, P(y/z)}.
В конечномерном случае, когда m и 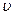 дискретно и конечно, то пространство выборок удобно рассматривать в виде таблицы, в которой строками являются состояния природы, столбцами — исходы эксперимента, а элементами — условные вероятности p
дискретно и конечно, то пространство выборок удобно рассматривать в виде таблицы, в которой строками являются состояния природы, столбцами — исходы эксперимента, а элементами — условные вероятности p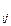 , которые определяют вероятности исхода y
, которые определяют вероятности исхода y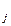 при состоянии природы z
при состоянии природы z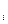 .
.
Пример: «задача о тест-контроле»
Состояния природы: z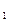 < ПДК
< ПДК
z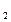 > ПДК
> ПДК
Три исхода: y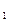 – вредных примесей не обнаружено;
– вредных примесей не обнаружено;
у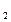 – вредных примесей обнаружено меньше ПДК;
– вредных примесей обнаружено меньше ПДК;
у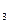 – вредных примесей обнаружено больше ПДК.
– вредных примесей обнаружено больше ПДК.
| z/y | P(y/z) | ||
| y1 | y2 | y3 | |
| z1 | 0,25 | 0,6 | 0,15 |
| z2 | 0,05 | 0,15 | 0,8 |
Очевидно, что при каждом исходе эксперимента, можно принимать какую-либо из гипотез.
|
|
|
y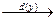 X = {x
X = {x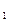 , x
, x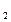 ,…, x
,…, x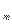 }
}
d(y) — решающая функция.
В играх без экспериментальных статистик решения принимают, исходя из априорных вероятностей состояния природы; статистик принимает решение, исходя из исхода эксперимента.
Чтобы формализовать задачу выбора своих решений, статистик должен заранее проанализировать все возможные исходы эксперимента и установить правило 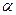 , позволяющее принимать решение x
, позволяющее принимать решение x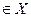 при каждом y
при каждом y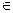 Y; d:
Y; d: 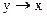 называют решающей функцией.
называют решающей функцией.
Пусть в задаче имеется возможность обрабатывать продукцию по технологиям x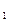 , x
, x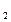 , x
, x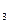 . Этот выбор должен осуществиться при исходах y
. Этот выбор должен осуществиться при исходах y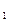 , y
, y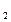 , y
, y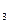 .
.
Решающая функция d(y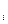 ) = x
) = x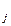 . Эту функцию можно описать в виде пар (i, j).
. Эту функцию можно описать в виде пар (i, j).
Варианты построения решений:
1. (1, 1), (2, 1), (3, 2);
2. (1, 1), (2, 2), (3, 2) и т. д.
Для анализа нужно рассматривать пространство D, образованное всеми возможными решающими функциями. Каждая решающая функция разбивает множество Y исходов эксперимента на непересекающиеся подмножества S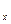 = {y: d(y) = x}
= {y: d(y) = x}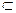 Y. Это непересекающееся множество можно определить для каждого x
Y. Это непересекающееся множество можно определить для каждого x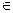 X. Для нашего эксперимента для первого случая S
X. Для нашего эксперимента для первого случая S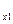 = {y
= {y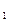 , y
, y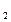 };
};
S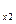 = {y
= {y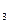 }; S
}; S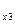 = {
= {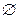 }. Аналогично можно сделать для каждой решающей функции.
}. Аналогично можно сделать для каждой решающей функции.
X = {x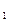 , x
, x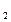 } — двухальтернативная задача. Решающая функция d(y) принимает два значения:
} — двухальтернативная задача. Решающая функция d(y) принимает два значения:
d(y) =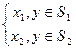 ; y = S
; y = S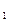
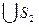 ; S
; S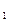
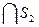 =
=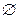
y в этом случае — критическая область.
Понятие «решающая функция» позволяет принимать (выбирать) такую из них, которая даёт наиболее выгодное решение. Возникает вопрос: как определить качество решающей функции? Качество решающей функции удобно оценивать с помощью функции риска.
 2014-02-02
2014-02-02 1021
1021








