Функции риска

Пусть задана решающая функция:

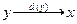
Очевидно тогда, каждому решению 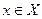состояния природы z будут соответствовать потери статистика L(z,x).

L(z,x)=L(z,d(y))=(z,d).

Они показывают потери статистика при состоянии z.

Исход у при данном состоянии природы z случаен и характеризуется вероятностью.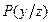

.

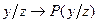Очевидно, что с этой же вероятностью будут получаться потери (z,d).

При определении качества d(y) нужно учитывать все у, появившиеся при данном z. Необходимо учитывать все возможные исходы эксперимента и вести речь о средних потерях.

Эти средние потери называют функцией риска.

Для оценки риска вводят следующую функцию:

.

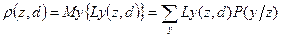Каждой решающей функции и каждому состоянию природы будут соответствовать свои значения функции потерь 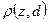на множестве 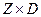, где Z — множество состояний природы, а D — множество решающих функций.

В играх с экспериментом статистик имеет возможность использовать не только чистые, но и смешанные стратегии.

Для формирования смешанной стратегии статистик должен использовать механизм случайного выбора решающих функций из 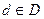. Для этого нужно задать 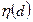— распределение вероятности решающей функции d при смешанной стратегии статистика в игре с единичным экспериментом.

Если это распределение задано, то

.

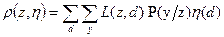Очевидно, что либо чистая стратегия, либо смешанная будут наилучшими, если они минимизируют средние потери.

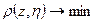
Пример: «Задача о тест-контроле продукции».

Пусть 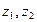— состояния природы.

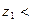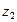ПДК;

>ПДК.

Исходы эксперимента:

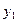— примесей нет, 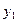=0.

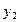— примесей<ПДК;

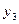— примесей>ПДК;

х — наше решение.

Тогда эту игру с природой можно описать следующей таблицей:

z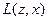
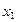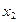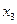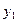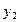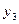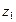				0,25	0,6	0,15
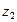				0,05	0,15	0,8

Так как d(y) принимает значения 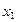,,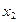, 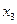то d(y)={,,}

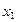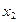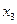Найдем для этой функции потери:

Для состояния :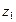

Для состояния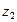

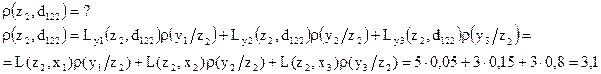
Такие же потери можно посчитать для любой другой (допустимой) решающей функции. Посчитанные таким образом значения можно представить графически на плоскости.