2014-02-02
405
Предположим, что в игре с единичным экспериментом множество чистых стратегий Х={
}, а множество исходов эксперимента У=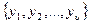
. Определим N — число всевозможных решающих функций, которые можно построить в этой ситуации.
Пусть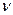 
=1 — один исход, 
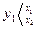, N=l — число решающих функций, которое можно принять в этой ситуации.
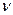=2,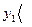 
, 
, 
.
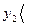Аналогично для 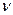=3, 
.
Для произвольных :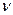 
.
Если l и 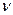существенны, то число всевозможных решений функции становится неприемлемо велико.
В литературе существует несколько подходов, позволяющих упростить эту задачу. Наиболее популярным из них является метод нахождения байесовских стратегий, когда априорные распределения вероятностей q(z) состояний природы z заменяются на апостериорные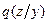 
. Число чистых стратегий статистика при этом не возрастает (в игре с единичным экспериментом). Это значит, что она равна числу чистых стратегий в игре без экспериментов.
