Термодинамика агрегатных превращений

План лекции: Уравнение Клайперона – Клаузиуса. Применение уравнения Клайперона – Клаузиуса к процессам испарения и возгонки. Зависимость давления насыщенного пара от температуры.

Фазовые переходы чистого вещества в двухфазной однокомпонентной системе представим следующим образом.

Фазовый переход:	Процесс:	При фазовом переходе:
α→β
Жидкость	Пар	Испарение	значительно изменяется объем;
Твердое	Пар	Возгонка
Твердое	Жидкость	Плавление	объем практически не изменяется;
Твердое	Твердое	Полиморфное превращение	(конденсированное состояние).

При равновеси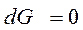и или .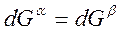

При этом 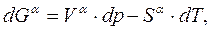(5.1)

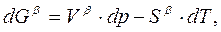(5.2)

где 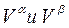- это мольные объемы вещества в фазах α и β,

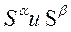- это энтропии вещества в фазах α и β.

Так как 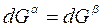, получаем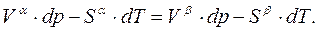

Объединяем объемы и энтропии:

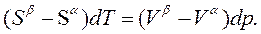(5.3)

Отсюда 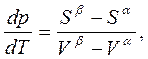(5.4)

где 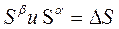- это изменение энтропии при фазовом переходе;

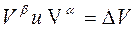- это изменение объема при фазовом переходе.

Так как 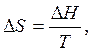получаем 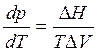, (5.5)

где 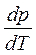- изменение давления насыщенного пара с температурой.

Уравнение (5.5) - это уравнение Клаузиуса-Клайперона,

Применение уравнения Клаузиуса-Клайперона к процессам испарения и возгонки.

«Жидкость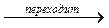пар» или «твердое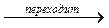пар».

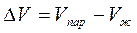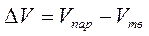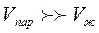или .

или .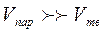

Объемом конденсированного состояния (жидкости, твердого) можно пренебречь по сравнению с объемом пара и считать: .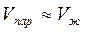

Предложим, что пар подчиняется законам идеального газа, тогда 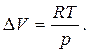Подставляем это выражение в уравнение (5.5): , получаем: 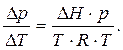Так как 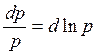, получаем

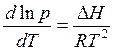. (5.6)

Это уравнение Клаузиуса-Клайперона для процессов испарения и выгонки. Физический смысл уравнения: с ростом температуры давление насыщенного пара в системе растет.

При 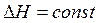можно из уравнения Клаузиуса-Клайперона найти значение величины теплового эффекта и равновесного давления насыщенного пара. Преобразуем уравнение (5.6), получаем

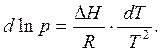(5.7)

Берем неопределенный интеграл выражения (5.7), после интегрирования:

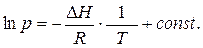(5.8)

Уравнение (5.8) отвечает уравнению прямой линии. Построим графическую зависимость 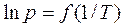, рис. 2. Из графика находим тангенс угла наклона α: 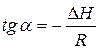, тогда .

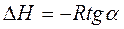Рис. 2. Графическая зависимость

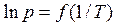
Возьмем определенный интеграл выражения (5.7), получаем:

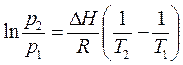. (5.9)