ПФ любого звена или системы представляет собой отношение двух полиномов: 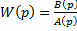 ; корни уравнения
; корни уравнения 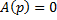 - это полюсы, корни уравнения
- это полюсы, корни уравнения 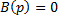 - это нули.
- это нули.
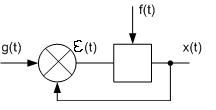
Так как любая система состоит из отдельных динамических звеньев, то для получения описания всей системы необходимо получить ДУ, описывающие все эти звенья, и после линеаризации (преобразование Лапласа) систему можно представить в виде:
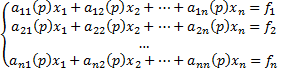
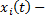 обобщенные координаты системы (все внутренние сигналы системы), в том числе выходной сигнал
обобщенные координаты системы (все внутренние сигналы системы), в том числе выходной сигнал 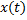 и сигнал ошибки
и сигнал ошибки 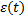 .
. 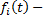 задающие и возмущающие воздействия, в том числе
задающие и возмущающие воздействия, в том числе 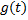 и
и  .
.
Если решать эту систему относительно выходного сигнала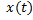 и задающего сигнала
и задающего сигнала 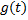 , то получим ДУ вида:
, то получим ДУ вида:

Если решать эту систему относительно выходного сигнала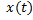 и сигнала ошибки
и сигнала ошибки 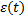 , то получим ДУ вида:
, то получим ДУ вида:
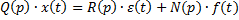
Если решать эту систему относительно 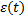 и
и 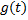 , то получим ДУ вида:
, то получим ДУ вида:
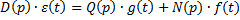
Из этих трех ДУ получим ПФ (не будем учитывать  ).
).
Из первого уравнения ПФ замкнутой системы: 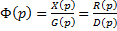
Из второго уравнения ПФ разомкнутой системы: 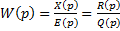
Из третьего уравнения ПФ по ошибке: 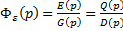
Характеристический полином замкнутой системы 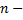 го порядка:
го порядка: 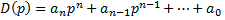 .
.
Характеристический полином разомкнутой системы 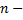 го порядка:
го порядка: 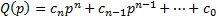 .
.
Характеристический полином числителя 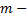 го порядка (
го порядка (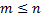 для возможности технической реализации):
для возможности технической реализации): 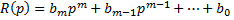 .
.
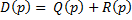


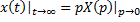
В установившемся режиме после окончания переходных процессов
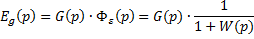
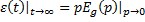
Ошибка от сигнала возмущения  :
: 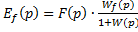 . Это ПФ от места приложения
. Это ПФ от места приложения  до выхода системы
до выхода системы
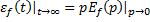
Зная ПФ системы всегда можно получить ДУ, связывающее вход и выход системы. Пример:
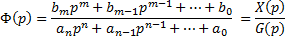
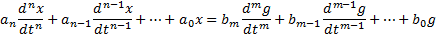
 2014-02-02
2014-02-02 926
926








