Классификация систем управления
Цели и задачи управления. Классификация систем управления.
ТУ – наука, изучающая законы управления, принципы управления, принципы построения систем управления, а также методы анализа и синтеза систем управления.
В зависимости от участия человека в управлении выделяют:
1) ручное (закон управления формируется человеком);
2) автоматическое (закон управления формируется без участия человека);
3) автоматизированное управление (сочетание первых двух: человек выбирает вариант управления на этапе принятия решения).
Любая система управления состоит из двух частей: объекта управления и управляющего устройства.
Простейший вариант:
(2.1)
Чаще используется элемент обратной связи:
(2.3.б) 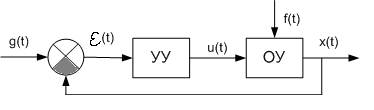
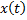 – управляемая выходная величина
– управляемая выходная величина
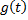 - задающее воздействие
- задающее воздействие
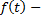 возмущающее воздействие
возмущающее воздействие
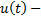 управляющее воздействие
управляющее воздействие
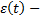 сигнал ошибки.
сигнал ошибки. 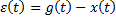
1. По количеству входов и выходов
1)одномерные системы (1 вход и 1 выход)
2)многомерные системы (несколько входов и/или несколько выходов)
2. По принципу действия
1) разомкнутые системы (Рисунок (2.1))
Хорошо работают только при выполнении условий:
-имеется достаточно информации о свойствах объекта
- незначительное количество или полное отсутствие помех
2) системы компенсации (управление по возмущению)
Недостаток: необходимость измерения или априорного задания возмущения
(2.2) 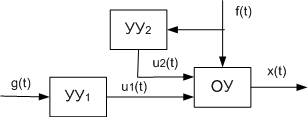
3) замкнутые системы
а) 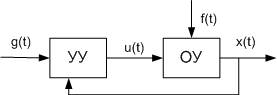
Недостаток: канал обратной связи является наиболее уязвимым местом и при его нарушении система может стать неработоспособной
б) Рисунок (2.3.б)
4) комбинированные системы
Пример: обратная связь + управление по возмущению:
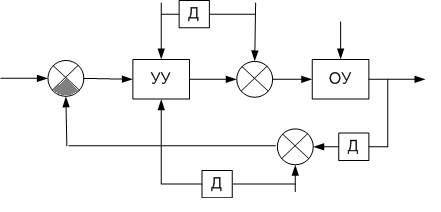
Д – датчик
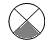 – отрицательная обратная связь (отрицательный сумматор)
– отрицательная обратная связь (отрицательный сумматор)
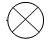 – простой сумматор
– простой сумматор
5)адаптивные системы:
Системы в процессе работы адаптируются к изменяющимся внешним условиям (Устройство управления состоит из нескольких устройств управления).
3. По задачам управления:
1) системы стабилизации: 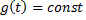 (например, поддержание температуры);
(например, поддержание температуры);
2) системы программного управления: 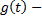 функция времени и заранее известна (т.е. решение по определенному алгоритму);
функция времени и заранее известна (т.е. решение по определенному алгоритму);
3) следящие системы: 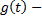 изменяется во времени, но заранее неизвестна.
изменяется во времени, но заранее неизвестна.
4. По виду уравнений в системе:
1) стационарные и нестационарные системы (в стационарных все параметры объекта и регулятора остаются постоянными, нестационарных параметры меняются во времени);
2)линейные и нелинейные системы (линейные описываются линейными уравнениями (алгебраическими, дифференциальными, конечно-разностными), нелинейные – нелинейными дифференциальными уравнениями).
5. По характеру передачи сигнала:
1) непрерывные (все координаты и переменные – непрерывные функции времени);
2) дискретные (системы, в которых имеется хотя бы один квантователь сигнала по времени).
Замечание: любая вычислительная система – дискретная
6. По характеру процессов в системе:
1) детерминированные системы – те системы, в которых нет случайных процессов (если подавать на вход одно и то же, то на выходе тоже будет одинаково);
2) стохастические – системы, в которых есть случайные процессы (анализировать работу системы по одной реализации невозможно, для получения характеристик необходимо выполнить несколько опытов и характеристики определятся как некоторое среднее).
7. По критерию качества системы:
1) с заданным качеством (без изменения принципа управления);
2) оптимальные (регулятор (УУ) строится так, чтобы обеспечить мин/макс какого-то критерия качества);
3) адаптивные (закон управления меняется при изменении условий).
Функциональная схема системы управления
Для выполнения задач управления любая система должна содержать минимальный необходимый набор функциональных элементов:
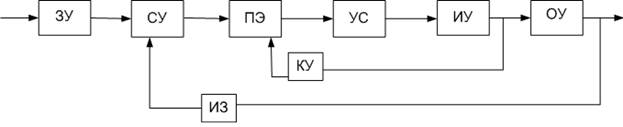 ЗУ – задающее устройство
ЗУ – задающее устройство
СУ – сравнивающее устройство
ПЭ – преобразовательный элемент (для согласования различных частей системы)
УС- усилитель
ИУ – исполнительное устройство
ОУ – объект управления
КУ – корректирующее устройство (местная обратная связь) для улучшения динамических свойств управления
ИЗ – измеритель (или датчик) фиксирует (измеряет) сигнал.
Классический пример: система стабилизации скорости двигателя постоянного тока
Электрическая схема:
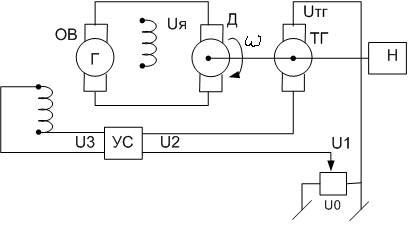
Структура:

1) для двигателя (Д): 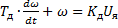 , где
, где  постоянная времени,
постоянная времени,  коэффициент передачи.
коэффициент передачи.
2) тактовый генератор (ТГ): 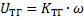 , где
, где 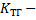 коэффициент пропорциональности
коэффициент пропорциональности
3) устройство сравнения ( ):
): 
4) усилитель (УС) – линейное звено: 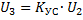
5) генератор (Г): 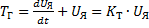 , где
, где 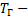 постоянная времени,
постоянная времени,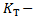 коэфф-т предачи.
коэфф-т предачи.
Решая относительно входа 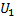 и выхода
и выхода 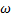 , т.е. исключая промежуточные переменные, получим ДУ, которое описывает работу данной системы.
, т.е. исключая промежуточные переменные, получим ДУ, которое описывает работу данной системы.
Передаточные функции (ПФ):
1) Для Д: 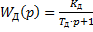 ,
, 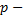 оператор Лапласса (
оператор Лапласса ( ),
), 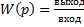
2) для ТГ:
3)для  – нет
– нет
4) для УС: 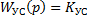
5) для Г: 
Любую структурную схему можно преобразовать к виду:
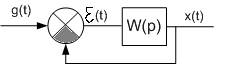
Тогда описание всей схемы: 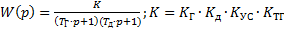
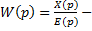 ПФ разомкнутой системы
ПФ разомкнутой системы
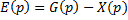 - это ошибка
- это ошибка
Решая уравнение относительно входа и выхода, получим ПФ замкнутой системы: 
ПФ– отношение изображения по Лапласу выходной величины к изображению по Лапласу входной величины при нулевых начальных условиях.
Преобразование Лапласа позволяет заменить решение ДУ алгебраическими вычислениями.
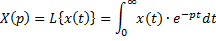
Оператор Лапласа: 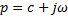
Свойства преобразования:
1) 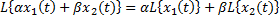
2) дифференцирование оригинала: 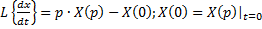
3) интегрирование оригинала: 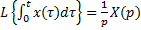
4) временной сдвиг: 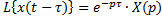
5) теорема о конечном значении: 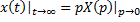 ;
; 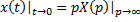
6) формула свертки: 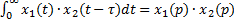
7) теорема обращения:
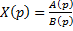 ;
;
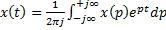 – обратное преобразование Лапласа.
– обратное преобразование Лапласа.
На практике используют формулу: 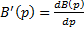
 2014-02-02
2014-02-02 561
561







