2014-02-04
751
Первоначально метод динамического программирования был разработан для дискретных систем. Как отмечалось ранее (см. п.2.3), дискретные объекты управления описываются не дифференциальными, а разностными уравнениями состояния:
, 
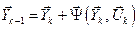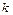=0, 1, 2, ….
Для одномерного объекта
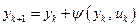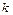, =0, 1, 2, …, (5.1)
где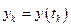 
, 
.
Для дискретного объекта критерий оптимальности имеет вид:
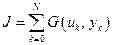. (5.2)
Рассмотрим задачу с закрепленным левым концом, для которой задано начальное состояние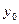 
и область допустимых управлений 
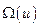. Необходимо найти такую последовательность управлений 
, 
, …, 
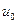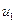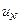, при которых критерий оптимальности 
(5.2) достигает минимального значения.
Решение задачи начинают с правого конца.
Предположим, что все управления , , …,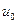 
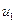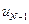найдены, а по формуле (5.1) найдены переменные состояния 
, …, 
(
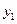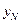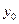задано по условию). Необходимо найти только 
.
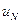Так как критерий оптимальности (5.2)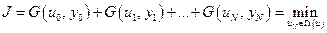 
и нам неизвестно только 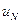, то, согласно принципу оптимальности (см. п.5.1), конечный участок оптимальной траектории также является оптимальным. Математически это можно записать в виде следующего выражения:
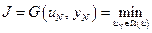. (5.3)
Теперь задача заключается в нахождении оптимального управления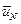 
(
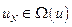), при котором выполняется уравнение (5.3). Причём, оптимальное управление 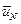будет зависеть от состояния 
(какое состояние такое будет и управление), т.е.
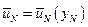. (5.4)
Обозначим через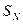 
минимальное значение 
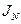, достигаемое при оптимальном управлении 
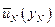, т.е.
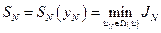. (5.5)
Для того чтобы найти оптимальное управление 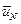необходимо взять частную производную т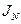о по 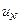и приравнять к нулю 
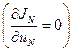. Однако часто оптимальное управление 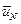оказывается за пределами области допустимых управлений 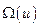. Для того чтобы найти оптимальное управление 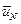из области 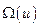(пусть не самое оптимально из всех управлений 
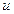, но оптимально из области 
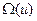) используются численные методы с помощью ЭВМ.
Решение задачи можно разбить на три этапа:
Этап 1. В области допустимых управлени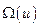й при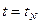 
проводим горизонтальный отрезок от её начала до конца (рис. 5.2). Разбиваем его на (
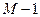) участков с шагам 
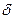. Тогда управление 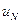может принимать только дискретные значения 
, 
, …, 
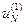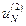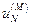. Шаг 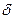выбирают достаточно малым, чтобы точность расчётов была высокой.
 |
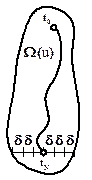Рисунок 5.2 – Разбиение области допустимых управлений 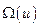на 
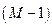отрезков с шагом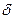
Аналогично разбивается и диапазон допустимых состояний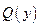 
на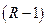 
отрезков с шагом 
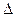при .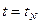
 |
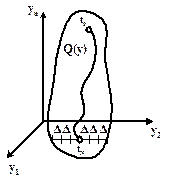Рисунок 5.3 – Разбиение области допустимых состояний 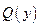на 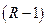отрезков с шагом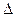
Далее ищут критерий оптимальности 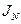(5.3) в точке 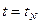вначале для первого значения переменной состояния 
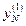горизонтального отрезка области допустимых состояний 
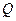. Для этого при фиксированном 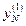, подставляя различные 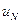, вычисляют последовательность 
, 
, …, 
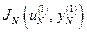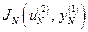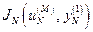. Из этой последовательности 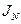определяют минимальное значение и обозначают его 
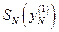(см.(5.5)), а управление - 
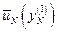(см.(5.4)).
Таким образом, в памяти ЭМВ остаются три величины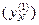 
, 
,
.
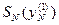Далее берётся следующее значение переменной состояния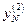 
в точке 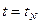и выполняются такие же действия. Все операции повторяются до последней точки 
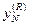горизонтального отрезка области допустимых состояний 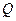. В результате в памяти машины хранятся значения переменных состояния 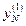, , 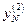…, 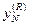и соответствующих им оптимальных управлений 
, 
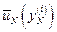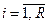в точке .
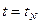Этап 2. Следующим этапом является нахождение оптимальных управлений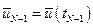 
для предыдущей 
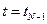точки. В этой точке критерий оптимальности 
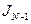будет зависеть не только от значени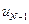й и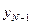 
, но и от последующих 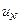и , а именно:
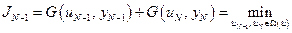(5.6)
Минимальное значение второго слагаемого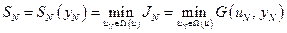 
уже было найдено на предыдущем этапе. Тогда условие (5.6) можно переписать в следующем виде:
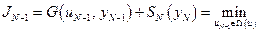. (5.7)
Из (5.7) видно, что критерий качества 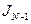не зависит от управления 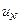в точке 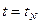, но зависит от переменной состояния 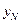. Для снятия этой зависимости можно воспользоваться разностным уравнением (5.1), записанным в виде:
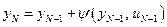. (5.8)
Следовательно, критерий (5.7) можно переписать следующим образом:
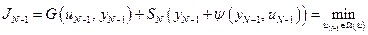. (5.9)
Аналогично (5.4) оптимальное управление в точке 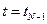обозначим
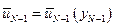. (5.10)
Тогда минимальное значение критерия 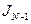в точке 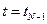, аналогично (5.5), обозначим 
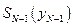. С учётом введённых обозначений выражение для 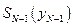примет вид:
. (5.11)
Из выражения (5.11) видно, что минимальное значение критерия 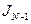в точке 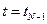зависит только от 
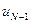и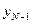 
.
В этом случае, при 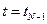, как и в точке 
, область допустимых управлений 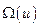разбиваем на 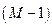, отрезков, а область допустимых состояний 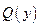- на 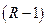отрезков, на концах которых отмечают точк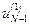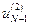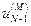и 
, 
, …, 
и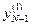 
, 
, …, 
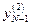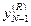соответственно.
На основании формулы (5.8) находим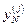 
при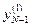 
и каждом 
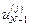, т.е.:
, 
.
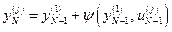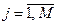Рассчитанное значение 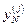округляют до ближайшего 
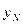, полученного на первом этапе, и из памяти машины извлекают величину 
, соответствующую .
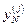В результате при 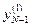и разных 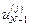, , 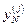формируется система
, .
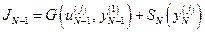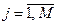Записав 
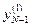выражений при , ищется минимальное 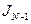, которое обозначается 
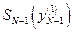. В память машины записывается , 
, 
.
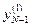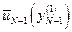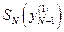Потом действия повторяются при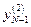 
, …, 
.
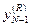В результате в памяти машины окажутся записанные состояния 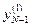, , 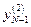…, 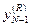; оптимальные управления 
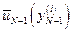и минимальные значения критерия качества 
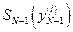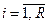, . При этом информацию об минимальных значениях критерия качества в точке 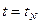из памяти машины можно убрать.
Аналогичные операции проводятся для переменных состояния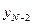 
и т.д.
Дойдя до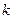 
- го шага выражение (5.11) примет следующий вид:
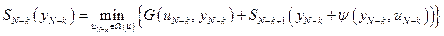. (5.12)
Оптимальное управление, аналогично (5.10) можно записать следующим образом:
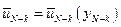. (5.13)
Придавая 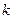возрастающие значения, дойдем до 
.
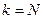Для этого случая
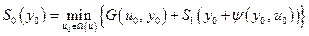. (5.14)
Как и в случае (5.10), из (5.14) находим оптимальное управление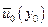 
и величину 
как функции от заданного состояния объекта 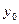. Эта операция выполняется аналогично операции, описанной для точки 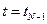, только переменная 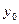принимает одно значение, а управления 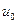– значений: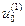 
, 
, …, 
.
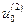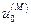Этап 3. Зная 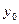и определив оптимальное управление 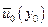, по формуле (5.1) рассчитывается 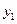. Из хранящихся в памяти машины переменных состояния 
, 
, …, 
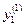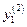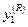выбирается ближайшая к переменной 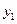, рассчитанной по формуле (5.1). В памяти машины каждой переменной 
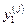хранится соответствующее ей оптимальное управление 
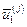, т.е., зная 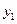, находим 
.
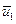По формуле (5.1) вычисляется переменная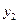 
. Далее все операции повторяются до 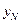. В итоге находим всю последовательность оптимальных управлений , 
, …, .
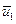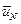Метод динамического программирования в дискретном варианте не является средством аналитического решения задачи, но легко реализуется с помощью ЭВМ. Достоинство метода: чем больше ограничений и уже область допустимых управлений, тем меньше вычислений требуется выполнить.
Этот метод может быть применен и для многомерных объектов, но тогда количество вычислений увеличивается. Это обстоятельство известно под названием «проклятия размерности».
