Для простоты рассмотрим случай одномерного управления. Представим, что оптимальное управление 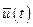 при начальных условиях (6.9) известно. Пусть до времени
при начальных условиях (6.9) известно. Пусть до времени 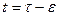 неоптимальное
неоптимальное  и оптимальное
и оптимальное 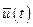 управления совпадают (рис. 6.1), а на отрезке времени
управления совпадают (рис. 6.1), а на отрезке времени 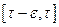
 они отличаются на величину
они отличаются на величину 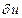 , т.е.
, т.е.
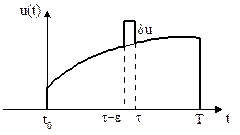 |
 .
.
Рисунок 6.1 - Отличие оптимального 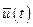 и неоптимального
и неоптимального  управлений на отрезке времени
управлений на отрезке времени 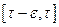 на величину
на величину 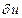
Далее, на отрезке  неоптимальное и оптимальное управления снова совпадают. Пусть отрезок
неоптимальное и оптимальное управления снова совпадают. Пусть отрезок 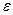 является бесконечно малым.
является бесконечно малым.
Теперь рассмотрим траекторию движения объекта при оптимальном и неоптимальном управлениях (рис. 6.2).
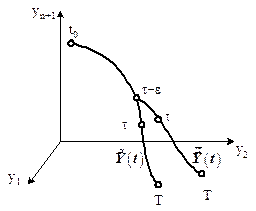 |
Рисунок 6.2 - Траектории движения объекта при оптимальном и неоптимальном управлениях
Как видно из рис. 6.2, до точки  оптимальная
оптимальная 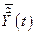 и неоптимальная
и неоптимальная 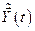 траектории движения совпадают. Различие в управлении на отрезке
траектории движения совпадают. Различие в управлении на отрезке 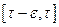 вызывает различие оптимальной
вызывает различие оптимальной 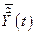 и неоптимальной
и неоптимальной 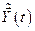 траекторий движения при
траекторий движения при  .
.
Обозначим отклонение вектора состояния 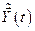 от оптимального
от оптимального 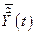 через
через  :
:
 , (6.11)
, (6.11)
где 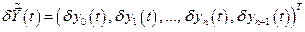 .
.
На бесконечно малом отрезке 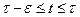 траекторию можно считать линейной в силу малости
траекторию можно считать линейной в силу малости 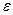 . Тогда при
. Тогда при  отклонение
отклонение  можно записать, используя разложение в ряд Маклорена:
можно записать, используя разложение в ряд Маклорена:
|
|
|
 . (6.12)
. (6.12)
Поскольку 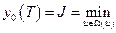 является критерием качества, то отключение от критерия качества также должно быть минимальным, т.е.
является критерием качества, то отключение от критерия качества также должно быть минимальным, т.е.
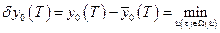 . (6.13)
. (6.13)
Условие (6.13) можно переписать следующим образом:
 . (6.14)
. (6.14)
Если ввести 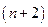 -мерный вектор
-мерный вектор
 , (6.15)
, (6.15)
то условие (6.14) примет вид:
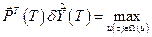 . (6.16)
. (6.16)
Для произвольных 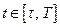 можно подобрать такой вектор
можно подобрать такой вектор 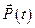 , чтобы выполнялось условие
, чтобы выполнялось условие
 . (6.17)
. (6.17)
Поскольку 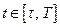 , то при
, то при 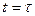 можно записать, что
можно записать, что
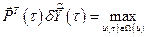 . (6.18)
. (6.18)
Подставив (6.12) в выражение (6.18), получим:
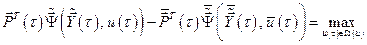 . (6.19)
. (6.19)
Здесь 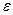 не зависит от
не зависит от  , поэтому его можно сократить.
, поэтому его можно сократить.
Так как 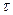 может быть выбрана на любом участке
может быть выбрана на любом участке  , то
, то 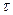 можно заменить на
можно заменить на 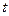 . Тогда выражение (6.19) примет вид:
. Тогда выражение (6.19) примет вид:
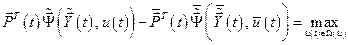 .
.
Поскольку второе слагаемое соответствует оптимальному управлению 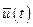 и не зависит от неоптимального управления
и не зависит от неоптимального управления  , т.е. является постоянным при любом
, т.е. является постоянным при любом  , то чтобы выполнялось условие максимума необходимо, чтобы максимальным было первое слагаемое. Следовательно,
, то чтобы выполнялось условие максимума необходимо, чтобы максимальным было первое слагаемое. Следовательно,
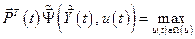 . (6.20)
. (6.20)
Обычно произведение 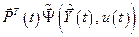 записывают как аргумент какой-то функции, например
записывают как аргумент какой-то функции, например 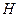 :
:
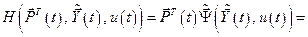
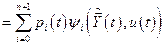 , (6.21)
, (6.21)
где 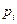 ,
, 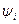 - компоненты векторов
- компоненты векторов 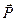 и
и 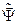 .
.
Функцию 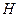 называют функцией Гамильтона или гамильтонианом.
называют функцией Гамильтона или гамильтонианом.
Следовательно, принцип максимума Понтрягина формулируется следующим образом: для того, чтобы в задаче с закреплённым левым концом траектории 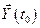 свободным правым концом траектории
свободным правым концом траектории 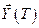 и фиксированным временем управления
и фиксированным временем управления 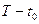 управление
управление  было оптимальным, необходимо существование такой непрерывной ненулевой векторной функции
было оптимальным, необходимо существование такой непрерывной ненулевой векторной функции 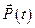 , чтобы при любых
, чтобы при любых 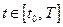 функция
функция 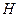 , представляющая скалярное произведение вектора скорости движения точки
, представляющая скалярное произведение вектора скорости движения точки 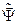
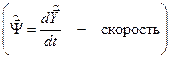 на вектор
на вектор 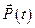 , достигала максимума по управлению
, достигала максимума по управлению  , т.е. необходимо, чтобы выполнялось условие
, т.е. необходимо, чтобы выполнялось условие
|
|
|
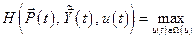 (6.22)
(6.22)
и в конечный момент времени  имело место соотношение:
имело место соотношение:  .
.
Оптимальное управление 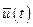 получено для разомкнутой системы. Для перехода к замкнутой системе необходимо, чтобы оптимальное управление
получено для разомкнутой системы. Для перехода к замкнутой системе необходимо, чтобы оптимальное управление 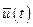 зависело только от
зависело только от 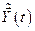 , т.е.
, т.е. 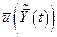 . Для многомерного управления вместо скаляра
. Для многомерного управления вместо скаляра 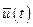 используется вектор
используется вектор 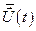 .
.
6.3 Система сопряжённых уравнений
При выводе принципа максимума был введен вектор 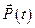 , который ещё не был определён. Для нахождения его выражение (6.17) продифференцируем по времени
, который ещё не был определён. Для нахождения его выражение (6.17) продифференцируем по времени 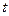 и приравняем к нулю:
и приравняем к нулю:
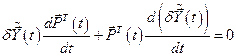 . (6.23)
. (6.23)
Упростим (6.23). Для этого разложим второе слагаемое (6.23) в ряд Тейлора*:
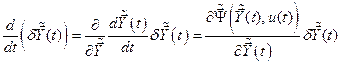 . (6.24)
. (6.24)
С учётом (6.24) выражение (6.23) примет вид:
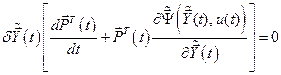 .
.
*Разложение в ряд Тейлора приведено в приложении А
Так как  , то
, то
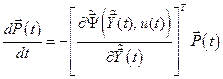 (6.25)
(6.25)
или в скалярной форме:
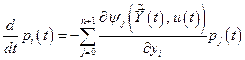 , (6.26)
, (6.26)
где 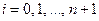 .
.
Система (6.25), (6.26) называется сопряжённой по отношению к системе уравнений объекта (6.8).
Из выражения (6.26) можно найти компоненты 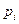 , используя уравнение состояния (6.8)
, используя уравнение состояния (6.8) 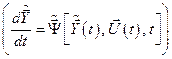 , выражение для функции Гамильтона (6.22) и граничное условие
, выражение для функции Гамильтона (6.22) и граничное условие  .
.
Из выражений (6.25) и (6.21) видно, что
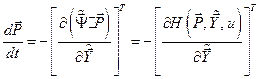 ,
,
а из (6.8) и (6.22) получается, что
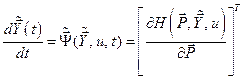
или в скалярной форме
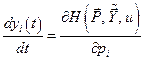 ;
; 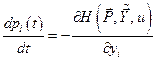 ,
, 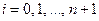 . (6.27)
. (6.27)
Соотношения (6.27) называются каноническими уравнениями Гамильтона.
 2014-02-04
2014-02-04 554
554








