Принцип максимума Понтрягина может быть использован для поиска оптимального управления и дискретных объектов. Рассмотрим задачу оптимизации для автономного объекта (без явной зависимости от времени 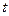 ) с фиксированным временем, одномерным управлением
) с фиксированным временем, одномерным управлением  со свободным правым концом траектории.
со свободным правым концом траектории.
Пусть объект управления описывается системой нелинейных разностных уравнений
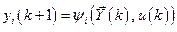 ;
; 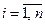 ;
; 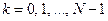 , (6.28)
, (6.28)
где 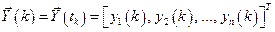 - вектор состояния;
- вектор состояния;
и заданы начальное состояние объекта 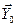 и ограничения на управления
и ограничения на управления 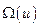 . Показатель качества
. Показатель качества
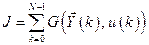 . (6.29)
. (6.29)
Необходимо найти такую последовательность управлений 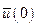 ,
, 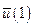 , …,
, …, 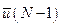 , принадлежащих области допустимых управлений
, принадлежащих области допустимых управлений 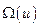 , при которых показатель качества
, при которых показатель качества  (6.29) достигает минимального значения, а траектория движения объекта управления проходит через заданную начальную точку
(6.29) достигает минимального значения, а траектория движения объекта управления проходит через заданную начальную точку 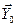 .
.
Как и в случае непрерывной задачи введём новую переменную 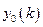 , удовлетворяющую уравнению
, удовлетворяющую уравнению
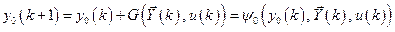 (6.30)
(6.30)
при нулевом начальном условии 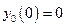 .
.
Из (6.30) видно, что при 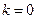
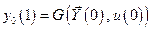 ;
;
при 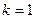
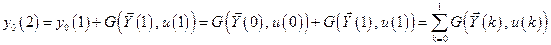 ;
;
при 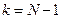
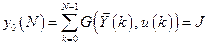 .
.
Поэтому задача сводится к минимизации значения компоненты 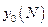 модифицированного вектора состояния объекта
модифицированного вектора состояния объекта 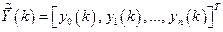 .
.
Для нахождения оптимального управления 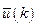 составляется функция Гамильтона
составляется функция Гамильтона
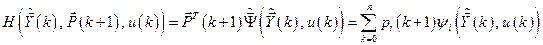 (6.31)
(6.31)
и система сопряжённых уравнений в векторной форме
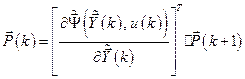 (6.32)
(6.32)
или в скалярной форме
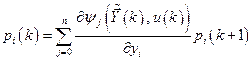 ,
, 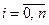 (6.33)
(6.33)
при граничных условиях 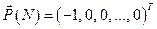 .
.
Управление 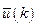 будет оптимальным, если функция Гамильтона
будет оптимальным, если функция Гамильтона 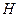 принимает максимальное значение:
принимает максимальное значение:
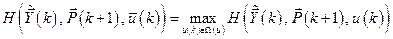 , (6.34)
, (6.34)
где вектор
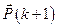 находится из уравнения (6.32) при граничном условии
находится из уравнения (6.32) при граничном условии 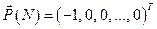 ;
;
вектор 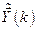 находится из (6.28) и (6.30) при заданном начальном условии
находится из (6.28) и (6.30) при заданном начальном условии 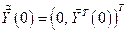 и
и 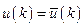 ;
;
функция Гамильтона 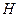 определяется в соответствии с (6.31).
определяется в соответствии с (6.31).
Соотношение (6.34) является необходимым условием минимума функционала  .
.
Вычисление оптимальных дискретных управлений 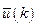 в соответствии с принципом максимума чаще решается с использованием ЭВМ и редко является аналитически решаемой задачей.
в соответствии с принципом максимума чаще решается с использованием ЭВМ и редко является аналитически решаемой задачей.
 2014-02-04
2014-02-04 1117
1117

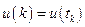 ;
; 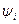 -
- 






