Модифицированный вектор состояния

ТЕМА 6 ПРИНЦИП МАКСИМУМА ПОНТРЯГИНА

Вопросы для самопроверки

1. В чём заключается принцип оптимальности при динамическом программировании?

2. Какая методика решения задач с закреплённым левым концом методом динамического программирования в дискретной задаче?

3. Какие этапы решения задач с закреплённым левым концом методом динамического программирования в дискретной задаче?

4. Как получается уравнение Беллмана в непрерывной задаче?

5. Какая методика определения оптимального управления в непрерывной задаче с помощью уравнения Беллмана?

Принцип максимума Понтрягина является одним из основных методов решения задач оптимального управления с закреплённым правым концом и фиксированным временем управления . Рассмотрим сущность метода.

Пусть объект управления описывается векторным дифференциальным уравнением

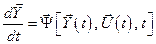(6.1)

и заданы начальное состояние объекта управления 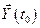, область допустимых управлений 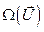и критерий качества

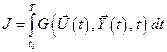. (6.2)

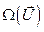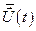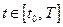Необходимо в классе допустимых управлений найти такое управление , при котором функционал на отрезке времени достигает минимального значения, т.е. выполняется условие:

.

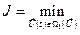Для решения задачи введём две дополнительные переменные:

1) переменная 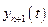, определяемая уравнением

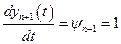, (6.3)

из которого следует, что ;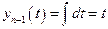

2) переменная 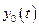, подчинённая уравнению

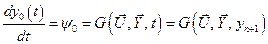. (6.4)

Из (6.4) видно, что 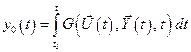. При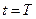

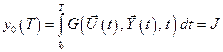. (6.5)

С учётом новых переменных 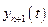и 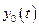введём 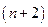-мерный модифицированный вектор состояния

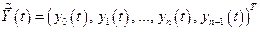(6.6)

и 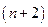-мерный вектор – функцию

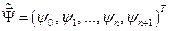. (6.7)

Тогда уравнение состояния (6.1) примет вид:

, (6.8)

а начальное условие при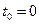

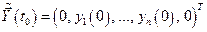. (6.9)

Следовательно, задачу оптимального управления можно сформулировать следующим образом: в классе допустимых управлений 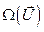найти такое управление, при котором траектория движения объекта пройдёт через начальную точку, а нулевая компонента вектора состояния 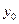в момент 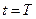примет наименьшее значение, т.е.

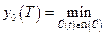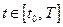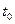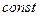; ; , =. (6.10)