Рассмотрим применение метода динамического программирования для непрерывной задачи.
Предположим, что оптимальное управление 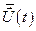 найдено и ему соответствует траектория движения объекта
найдено и ему соответствует траектория движения объекта 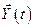 . Выберем на оптимальной траектории две точки, соответствующие моментам времени
. Выберем на оптимальной траектории две точки, соответствующие моментам времени 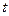 и
и 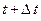 (рис. 5.4), где
(рис. 5.4), где 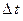 – малая величина.
– малая величина.
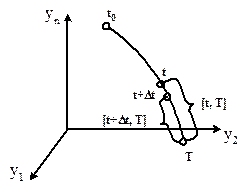 |
Рисунок 5.4 – Оптимальная траектория движения объекта
Тогда, согласно принципу оптимальности, участки оптимальной траектории от 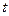 до
до  и от
и от 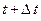 до
до  будут оптимальными. Как и в случае дискретной задачи, обозначим минимальное значение функционала
будут оптимальными. Как и в случае дискретной задачи, обозначим минимальное значение функционала 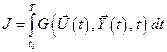 этих участков через
этих участков через 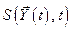 и
и  , соответственно:
, соответственно:
 ; (5.15)
; (5.15)
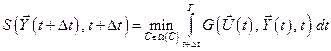 . (5.16)
. (5.16)
Определим, насколько изменяется минимальное значение функционала при переходе от точки 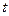 до
до 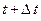 . Для этого из (5.15) вычтем (5.16):
. Для этого из (5.15) вычтем (5.16):
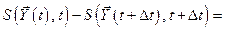
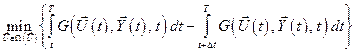 .
.
Откуда следует, что
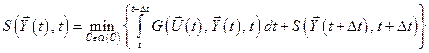 . (5.17)
. (5.17)
Учитывая, что 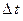 мало, то подынтегральная функция
мало, то подынтегральная функция 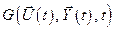 на малом отрезке
на малом отрезке 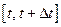 изменяется незначительно и её можно считать постоянной с какой-то погрешностью
изменяется незначительно и её можно считать постоянной с какой-то погрешностью 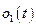 . Математически это можно записать следующим выражением:
. Математически это можно записать следующим выражением:
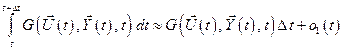 , (5.18)
, (5.18)
где 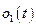 – малая величина, более малая чем
– малая величина, более малая чем 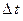 .
.
Теперь рассмотрим второе слагаемое в (5.17). Разложим функцию  в ряд Тейлора с учётом того, что
в ряд Тейлора с учётом того, что  зависит как от
зависит как от 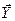 , так и от времени
, так и от времени 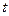 :
:
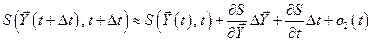 , (5.19)
, (5.19)
где 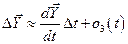 - разложение
- разложение 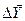 в ряд Тейлора;
в ряд Тейлора;
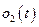 и
и 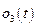 – совокупность последующих членов ряда Тейлора.
– совокупность последующих членов ряда Тейлора.
Подставив (5.18) и (5.19) в (5.17), получим:
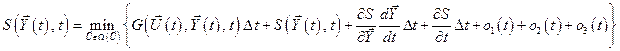 .
.
Сократим обе части на 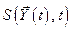 и поделим оставшееся выражение на
и поделим оставшееся выражение на 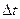 .
.
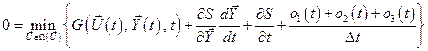 . (5.20)
. (5.20)
Проанализируем полученное уравнение (5.20). Так как 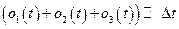 , то им можно пренебречь по сравнению с другими слагаемыми. Производная
, то им можно пренебречь по сравнению с другими слагаемыми. Производная  , также как и функция
, также как и функция 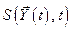 не зависит от управления
не зависит от управления 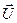 и может быть вынесена за фигурные скобки. Напомним, что согласно (2.23)
и может быть вынесена за фигурные скобки. Напомним, что согласно (2.23)
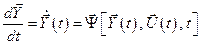 .
.
После выполнения всех указанных операций уравнение (5.20) перепишем следующим образом:
 . (5.21)
. (5.21)
Полученное уравнение (5.21) называется уравнением Беллмана в векторной форме.
В скалярной форме уравнение Беллмана имеет вид:
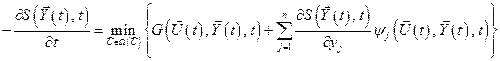 . (5.22)
. (5.22)
Уравнение Беллмана представляет собой дифференциальное уравнение в частных производных. Методика определения оптимального управления 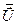 с помощью уравнения Беллмана сводится к следующим процедурам.
с помощью уравнения Беллмана сводится к следующим процедурам.
1. Из условия минимума выражения в фигурных скобках (5.21) находится оптимальное управление 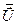 как функция
как функция 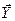 ,
,  ,
, 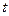 , т.е. в форме
, т.е. в форме 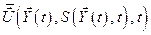 .
.
2. Найденное управление 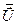 подставляется в выражение в фигурных скобках, что приведёт к новой форме уравнения, не содержащей управление
подставляется в выражение в фигурных скобках, что приведёт к новой форме уравнения, не содержащей управление 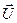 :
:
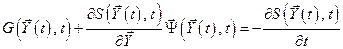 . (5.23)
. (5.23)
Это уравнение называется уравнением типа Гамильтона-Якоби.
3. При решении уравнения Гамильтона-Якоби (5.23) с учётом граничного условия 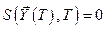 определяется функция
определяется функция 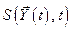 . Способы решения уравнения Гамильтона-Якоби в каждой задаче свои.
. Способы решения уравнения Гамильтона-Якоби в каждой задаче свои.
4. Определив функцию 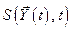 , подставляют её в выражение для оптимального управления
, подставляют её в выражение для оптимального управления 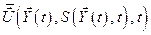 , полученного в пункте 1.
, полученного в пункте 1.
В результате получаем выражение для оптимального управления 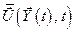 как функцию состояния
как функцию состояния 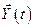 и времени
и времени 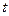 . Это и будет окончательное решение задачи.
. Это и будет окончательное решение задачи.
Полученное уравнение Беллмана (5.22) применимо к неавтономным (с обратной связью) системами, так как в нём присутствует явная зависимость от времени 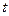 .
.
Для автономных систем, при отсутствии явной зависимости функции  от времени
от времени 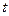 ,
, 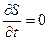 . Тогда уравнение Беллмана примет вид:
. Тогда уравнение Беллмана примет вид:
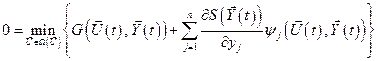 (5.24)
(5.24)
и методика вычислений упростится.
 2014-02-04
2014-02-04 1260
1260








