Метод итераций
Дана система нелинейных уравнений:
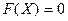
или
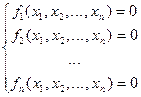 (1)
(1)
Допустим, что систему 1 можно привести к виду:
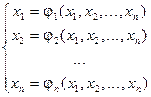 (2)
(2)
Введём обозначения:
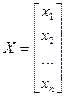 ,
, 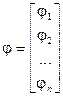 ,
,
Можно систему уравнений 2 переписать в виде:
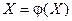
Приведённое матричное уравнение и есть формула метода итераций
Пусть функции 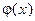 и
и 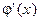 непрерывны в области
непрерывны в области 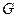 , причём в области
, причём в области 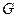 выполнимо неравенство:
выполнимо неравенство:
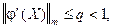
где 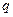 - некоторая константа.
- некоторая константа.
Если последовательные приближения
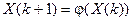 ,
, 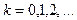
не выходят из области 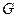 , то этот процесс сходится к единственному решению системы.
, то этот процесс сходится к единственному решению системы.
Следствие:
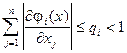
оценка пиближённо
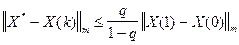
На практике лучше всего рассматривать матрицу с элементами
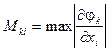
Для сходимости должно выполнятся условие
1) 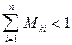
2) 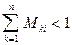
3) 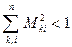
Метод скорейшего спуска (градиентный метод)
Дана система линейных уравнений:
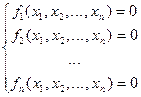 (1)
(1)
В матричном виде
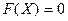
Считаем, что 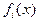 действительны и непрерывно дифференцируемы в их общей области определения.
действительны и непрерывно дифференцируемы в их общей области определения.
Рассмотрим функцию
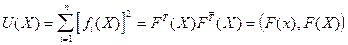 (2)
(2)
Очевидно, что если мы найдём решение системы уравнений 1 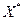 , то это решение является и решением системы уравнений 2 и наоборот.
, то это решение является и решением системы уравнений 2 и наоборот.
Предполагаем, что система 1 имеет лишь одно изолированное решение, представляющего собой точку строго минимум функции 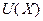 . Таким образом задача сводится к нахождению минимум функции
. Таким образом задача сводится к нахождению минимум функции 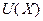 в
в 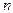 -мерном пространстве.
-мерном пространстве.
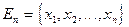
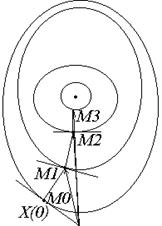
Берём точку  - нулевое приближение. Через точку
- нулевое приближение. Через точку  проходит поверхность уровня и
проходит поверхность уровня и 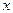 . Если
. Если  близка
близка 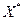 , то поверхность
, то поверхность 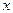 =
=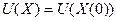 будет похожа на элипсоид.
будет похожа на элипсоид.
Из точки  движемся по нормали к поверхности
движемся по нормали к поверхности 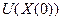 до тех пор, пока эта нормаль не коснётся
до тех пор, пока эта нормаль не коснётся 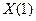 другой поверхности:
другой поверхности:
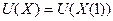
И так далее.
Так как  , то двигаясь таким образом, мы быстро приближаемся к точке с минимальным значением
, то двигаясь таким образом, мы быстро приближаемся к точке с минимальным значением 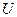 , которая соответствует некоему корню
, которая соответствует некоему корню 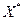 .
.
 2014-02-04
2014-02-04 258
258








