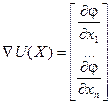
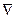 - набла или grad - есть вектор приложенный к точке
- набла или grad - есть вектор приложенный к точке 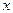 , имеющий направление нормали. Из векторных произведений
, имеющий направление нормали. Из векторных произведений
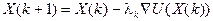 ,
, 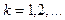 (3)
(3)
Как определить 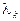 ? Для этого рассматривают скалярную функцию
? Для этого рассматривают скалярную функцию 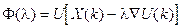 :
:
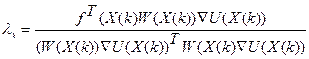
Уравнение 3 можно преобразовать так, чтобы не было явного выражения градиента. Введем обозначения 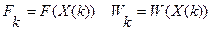 , тогда итерационная формула градиентного метода будет иметь вид:
, тогда итерационная формула градиентного метода будет иметь вид:
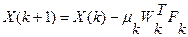 ,
,
где 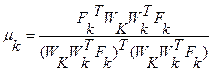
Вычисления производятся до тех пор, пока не станет справедливым следующее неравенство:
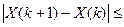 e,
e,
где e - заданная точность вычисления.
Пример. Дана система нелинейных уравнений:
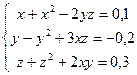
Найти решение системы градиентным методом с точностью e=0,01
Определим начальное приближение как:
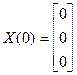
Вектор-функция 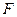 имеет вид:
имеет вид:
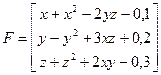
Якобиан, или матрица частных производных имеет вид:
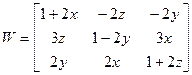
1 итерация

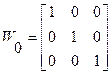
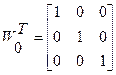
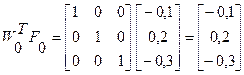
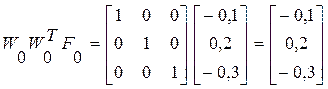
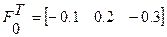
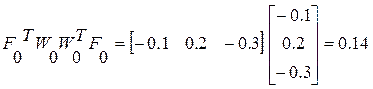
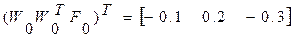
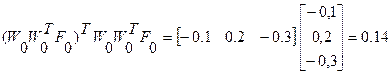

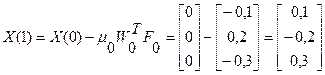
2 итерация
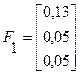
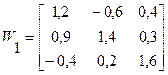
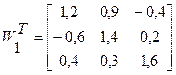
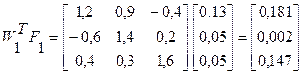
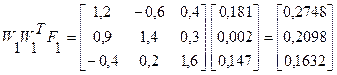
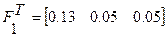
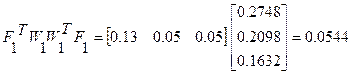
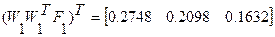

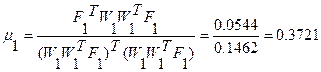
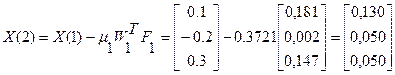
Решение системы нелинейных уравнений представлено в таблице:
| K | x | ½Dx½ | y | ½Dy½ | z | ½Dz½ |
| 0.000 | 0,100 | 0.000 | 0,200 | 0.000 | 0,300 | |
| 0.100 | 0,030 | -0.200 | 0,250 | 0.300 | 0,250 | |
| 0,130 | 0,095 | 0,050 | 0,251 | 0,050 | 0,209 | |
| 0,035 | 0,018 | -0,201 | 0,016 | 0,259 | 0,013 | |
| 0,017 | 0,003 | -0,185 | 0,007 | 0,246 | 0,001 | |
| 0,014 | -0,178 | 0,245 |
Таким образом, решение системы уравнений имеет вид:
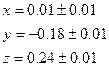
 2014-02-04
2014-02-04 344
344








