Сходимость градиентного метода
Сходимость метода гарантируется при выборе начального приближения вблизи 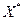 .
.
В любом случае метод может остановитья в точке относительного метода.
Обыкновенные дифференциальные уравнения (ОДУ) встречаются при описании движения системы взаимодействующих материальных носителей (механике, химической кинетике, электрических цепях, сопротивлении материалов и многих других явлениях жизни).Ряд важнейших задач сводится к задачам с обыкновенными дифференциальными уравнениями, а именно теория автоматического управления базируется на ОДУ, а также и другие курсы специальности АЭП
Простейшим ОДУ является уравнение 1-го порядка:
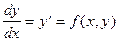
ОДУ n-го порядка имеет вид:
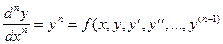

Однако любое уравнение n-го порядка можно свести к системе из n уравнений 1-го порядка:
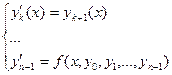
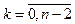
или
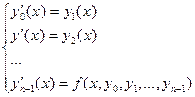
Таким образом, решение дифференциального уравнения n-го порядка сводится к решению системы дифференциальных уравнений 1-го порядка (количество дифференциальных уравнений в системе = n).
Если ввести следующие обозначения:

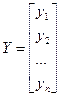

 ,
,
то систему дифференциальных уравнений можно переписать в векторно-матричном виде:
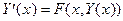 (1)
(1)
Известно, что система n-го порядка имеет множество решений,, которые в общем случае зависят от постоянных С, общее количество которых -n. Общее решение системы ОДУ может быть записано в виде:
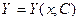 ,где
,где 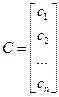
Для определения значения этих параметров, т.е. выделения единственного решения необходимо учитывать дополнительные условия. В зависимости от выбора дополнительных условий определены следующие типы задач для обыкновенных дифференциальных уравнений:
- задача Коши;
- краевая задача;
- задача на собственные значения.
 2014-02-04
2014-02-04 270
270







