Ключевые термины
Тема 3. Дифференциация и интеграция знаний
Ключевые термины
□ Теология
□ Интерпретация
□ Тавтология
□ Предвидение
□ Вероятность
□ Точечная оценка
В прошлом считалось, что развитие некоторой научной дисциплины идет путем непрерывного накопления все новых и новых научных истин (такой процесс называется кумуляцией). При этом возрастают точность и глубина знаний в этой дисциплине. Однако одновременно ослабевают связи с другими научными дисциплинами и дело доходит до того, что специалисты разных отраслей одной и той же науки нередко не понимают ни постановок задач, ни методов исследований, ни конечных результатов друг друга.
Дифференциация знаний - это процесс, связанный с более тщательным и глубоким изучением определенной области действительности (так называемый дисциплинарный подход). Однако необходим и междисциплинарный интегративный подход, обеспечивающий единство и целостность представлений.
Интеграция знаний - это процесс, связанный с использованием понятий, теорий и методов одной науки в смежных науках.
В результате интеграции возникают новые научные направления (например, биофизика, геохимия и пр.). Из смежных наук могут быть заимствованы тактика (приемы и методы) и стратегия (общие принципы) исследований, методология (способы получения новых знаний, анализа и оценки результатов исследований), порядок выполнения измерений и проведения экспериментов, математические модели и методы оценки их параметров.
Особое значение приобретает системный метод, позволяющий рассматривать с единых позиций предметы и явления в их взаимосвязи и целостности. Смежные науки позволяют в этом случае выделить элементы исследуемой системы, определить ее структуру. Поэтому системный метод является эффективным средством интегративных исследований.
| Дифференциация знаний |
| Интеграция знаний |
| Кумуляция знаний |
Основные законы (принципы) механики, сформулированные И. Ньютоном в своём главном труде «Математические начала натуральной философии» в 1687 году, заложили основу механической картины мира (макромира).
Ньютон создал основу науки как рационального способа познания мира. Одним из величайших результатов Ньютона было установление закона всемирного тяготения.
Этот закон гласит: Для точечных или сферически симметричных тел сила притяжения направлена по прямой, соединяющей тела. Все тела притягиваются друг к другу с силой, прямо пропорциональной массам взаимодействующих тел и обратно пропорциональной квадрату расстояния между ними.
Этот закон записывается в виде:
 (1)
(1)
Здесь m и M – массы тел,R – расстояние между точечными массами или между центрами сфер,G – гравитационная постоянная. Она характеризует гравитационное поле. В системе СИ G = 6,6720 ∙10-11 H∙м2/кг.
Закон однозначно констатировал:
- гравитационные силы свойственны всем телам по Вселенной, имеющим массу.
- гравитационные силы есть силы притяжения.
- источником сил являются массы тел. Масса в этом законе есть «масса тяготеющая».
- силы притяжения направлены «от центра к центру» и убывают при увеличении расстояния обратно пропорционально второй степени расстояния. С концептуальной точки зрения существенна, прежде всего «всемирность» закона. Закон прекрасно объясняет наблюдаемые траектории планет. Из него довольно просто можно было получить законы Кеплера. Осмысливая наблюдаемый характер движения небесных тел и тел на Земле, Ньютон сформулировал три основные законы механики.
Первый закон гласит: Всякое тело продолжает удерживаться в состоянии покоя или равномерного и прямолинейного движения, пока приложенными силами не изменит это состояние. По школьному курсу он известен всем как закон инерции. Из закона следует возможность идентичного описания механического движения в различных системах отсчёта, движущихся относительно друг друга равномерно и прямолинейно, то есть существование инерциальных систем отсчёта. В инерциальных системах все механические явления протекают одинаково, и все законы механики имеют единое толкование. Второй закон Ньютона связывает силу и изменение импульса системы. Напомним, что импульс тела 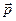 есть векторная величина, равная произведению массы тела m и векторного его скорости
есть векторная величина, равная произведению массы тела m и векторного его скорости 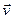 . Поэтому второй закон гласит: Изменение импульса пропорционально равнодействующей всех приложенных сил и происходит по направлению той прямой, по которой эта сила действует. Его математическая запись:
. Поэтому второй закон гласит: Изменение импульса пропорционально равнодействующей всех приложенных сил и происходит по направлению той прямой, по которой эта сила действует. Его математическая запись:
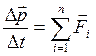 или
или 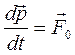 (2)
(2)
Это есть основное уравнение динамики поступательного движения. Считая массу тела постоянной и учитывая, что изменение вектора скорости в единицу времени есть ускорение тела  , основное уравнение можно представить в виде:
, основное уравнение можно представить в виде:
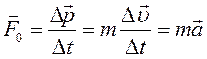 (3)
(3)
В этом уравнении 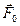 есть равнодействующая сила, а масса тела
есть равнодействующая сила, а масса тела 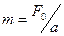 есть «масса инертная», или скалярная мера инертности тела, мера способности мела противостоять изменениям. Сила есть причина такого изменения. Равенство «массы тяготеющей» и «массы инертной» Ньютон принял без доказательств, как аксиому или постулат. Третий закон гласит: Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Математическая формулировка проста:
есть «масса инертная», или скалярная мера инертности тела, мера способности мела противостоять изменениям. Сила есть причина такого изменения. Равенство «массы тяготеющей» и «массы инертной» Ньютон принял без доказательств, как аксиому или постулат. Третий закон гласит: Действию всегда есть равное и противоположное противодействие, иначе – взаимодействия двух тел друг на друга между собой равны и направлены в противоположные стороны. Математическая формулировка проста:
 (4)
(4)
Заметим, что силы эти приложены к разным телам, поэтому складывать их нельзя.
Законы, открытые Ньютоном, составили основу механики. Чтобы их использовать, нужен был специальный язык. Ньютон сделал и это – он создал дифференциальное и интегральное исчисление, а также разработал основы «прикладной математики». Этот язык, в силу гениальной идеи, заложенной в его основу, зажил своей удивительной и плодотворной жизнью, став в наше время универсальным языком. Фактически Ньютон создал язык всей науки, а не только механики.
Механическое движение было сведено к точному математическому описанию: для этого необходимо и достаточно было задать начальные координаты тела, его скоростью (или импульс) и уравнение движения. Все последующие состояния движущегося тела точно и однозначно определялись в любой момент времени как в будущем, так и в прошлом, поскольку в поставленной таким образом задаче в уравнениях знак времени можно было менять на обратный (концепция обратимости времени).
Пример 3. Математическое описание механического движения тела
(по И. Ньютону).
Постановка задачи.
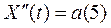 |
дифференциальное уравнение движения тела
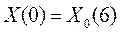
| начальная координата тела |  начальные условия начальные условия |
| начальная скорость тела |
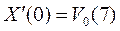 |
Требуется определить: зависимость x=x(t)
 2014-02-02
2014-02-02 2754
2754
