Рассеем некоторый замкнутый объём V ограниченно замкнутой поверхности S в котором существует электромагнитное поле.
Предположим, что это поле обладает энергией плотность которой u. Тогда полная энергия электромагнитного поля будет 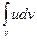
Вычислим 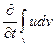 .
.
Изменение энергии в объёме V может происходить по двум причинам: за счёт переноса энергии через поверхность S и за счёт мощности всех сил действующих в системе. Смотри §2.4. Для вычисления переносим через поверхность S, введём вектор 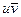 , где
, где 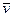 скорость переноса энергии, которая называется плотностью потока энергии.
скорость переноса энергии, которая называется плотностью потока энергии.
Тогда энергия переноса в единицу времени, через ds, будет 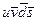 (смотри Электроток. Уравнение непрерывности). Так как это будет энергия, выносим из объёма
(смотри Электроток. Уравнение непрерывности). Так как это будет энергия, выносим из объёма 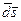 направленная наружу, то за единицу времени энергия в объёме уменьшится на величину -
направленная наружу, то за единицу времени энергия в объёме уменьшится на величину -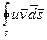 .
.
Если внутри объема V имеются электромагнитные заряды, то электронное поле будет совершать работу, что приведёт к уменьшению энергии поля (работа магнитного поля равна 0)
В § «Законы электрического тока» было показано, что мощность электромагнитных сил в единицу объёма вещества будет 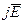 поэтому за единицу времени энергия электромагнитного поля в объёме V уменьшится на величину -
поэтому за единицу времени энергия электромагнитного поля в объёме V уменьшится на величину - 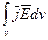
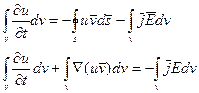
Так как это равенство должно выполняться для любого объекта V
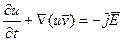
Рассмотрим уравнение Максвелла в сфере.
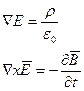
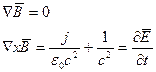
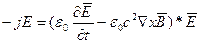
Рассмотрим 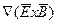
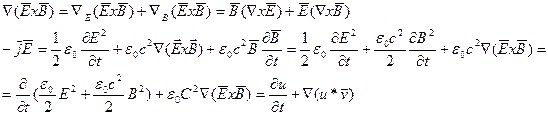
Сравнивая полученное выражения, находим, что плотность энергии электромагнитного поля будет
|
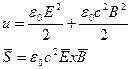
Для того чтобы убедится, что полученные результаты верны вспомни §2.13, что 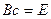 ,
,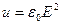 тогда
тогда 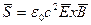
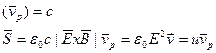
Таким образом электромагнитное поле обладает энергией, плотность которой 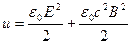
 2014-02-04
2014-02-04 758
758








