Принцип Ферма.
В §2.10 было показано, что любую произвольную волновую функцию можно записать в виде.
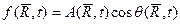 где
где 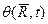 -фаза волны
-фаза волны
Поверхность в каждой точке, которой 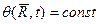 называется волновой поверхностью или волновым фронтом. В общем случае это произвольная поверхность.
называется волновой поверхностью или волновым фронтом. В общем случае это произвольная поверхность.
Разобьём эту поверхность на участки, такие, что их можно считать плоскими.

Если при этом размере участка будет много больше длинны волны, а время в течение которого этот участок остаётся плоским много больше периода волны, то можно говорить о приближение геометрической оптики рассмотрим один такой участок для начало систем координат поместим на этом участке и за начало отсчёта времени выберем 0
Разложим фазу колебаний в степенной ряд в окружности точки 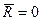 t = 0
t = 0
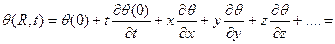
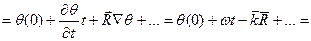
Приближение геометрической оптики рассмотрим участок волнового фронта можно считать частью плоской волны для которой фаза 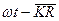 , а фазовая скорость
, а фазовая скорость 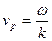 . Из этого следует что в приближение геометрической оптики при разложение в ряд фазы можно ограничить лишь первыми членами ряда
. Из этого следует что в приближение геометрической оптики при разложение в ряд фазы можно ограничить лишь первыми членами ряда
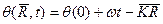
В этом приближение можно считать, что направление распространения произвольной волны совпадает с направление 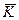 в каждой точке волнового фронта как в плоской волне, а скорость распространения фазы будет
в каждой точке волнового фронта как в плоской волне, а скорость распространения фазы будет 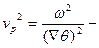 Уравнение Эйконала.
Уравнение Эйконала.
Лучом называют линию касательно к каждой точке которой является вектор К. Для определения формы луча очень полезен принцип Ферма для вывода которого рассмотрим разности фаз 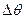 в двух точка распространяется на одном луче в один и тот же момент времени.
в двух точка распространяется на одном луче в один и тот же момент времени.

Эту разницу фаз модно вычислить интегрируя бесконечно малые изменения фазы вдоль луча
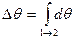
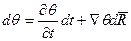
Так как 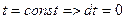
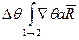
С другой стороны 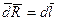
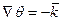
То есть градиент направлен по касательной к траектории точно также как и dl
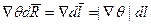
Из уравнения Эйконала
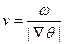
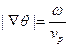
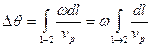
Интеграл 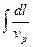 вычислим вдоль луча и равен времени распространения волны вдоль луча от 1 до 2.
вычислим вдоль луча и равен времени распространения волны вдоль луча от 1 до 2.
Заметим, что разность фаз в точках 1-2 величина постоянная и не зависит от способа её нахождения. Туже самую разность фаз можно по другой траектории не совпадает с лучом, но в этом случаи полученный результат будет неправильным так как 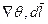 непараллельные
непараллельные
Выбирая каждый раз другую траекторию не совпадающий с лучом мы будем получать различные результаты, то есть 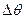 будет зависит от траектории и только тогда когда траектория совпадёт с лучом
будет зависит от траектории и только тогда когда траектория совпадёт с лучом 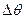 не зависит от формы траектории.
не зависит от формы траектории.
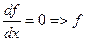 не зависит от х
не зависит от х
Условие независимости функции и условие её экстремума совпадает поэтому интеграл вычисленный вдоль луча не зависит от формы луча и является экстремальной.
Оказывается что на траектории луча это минимальная величина.
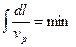 Время распределения волны вдоль луча минимально. Это и есть принцип Ферма.
Время распределения волны вдоль луча минимально. Это и есть принцип Ферма.
Рассмотрим форму луча между двумя точками в однородной среде.
В однородной среде во всех точках фазовая скорость волны будет постоянна
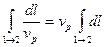
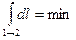 -длинна луча.
-длинна луча.
Таким образом в однородной среде луч между точкой 1 и 2 должен быть минимальной длины, то есть прямая линия.
Другими словами в однородной сфере лучи это прямые линии.
Рассмотрим форму луча между точками 1 и 2 находящихся в разных однородных сферах
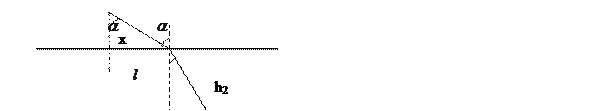
Так как в каждой сфере луч это прямая линия то общий луч будет состоять из двух прямых.
Время распространения волны от точки 1 до точки 2 будет
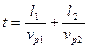
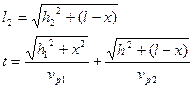

Так как время должно быть минимальным то 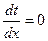
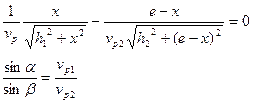
n- коэффициент преломления.
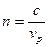 для электромагнитных волн
для электромагнитных волн
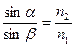
§2.13 Электромагнитные волны в вакууме.
Электромагнитное поле, как известно полностью описывает уравнение Максвелла которые в вакууме будут иметь вид
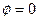
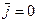
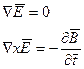
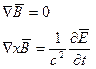
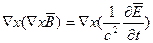
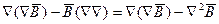
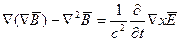
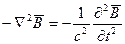
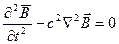
Уравнение для 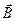 совпадает с волновым уравнением решение которого было найдено в § 2.1. Точно также:
совпадает с волновым уравнением решение которого было найдено в § 2.1. Точно также:
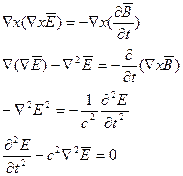
То есть мы получим волновое уравнение. Таким образом решение уравнения Максвелла в вакууме будет иметь вид волновых функций. Для простоты рассмотрим сначала случай гармонических волн.
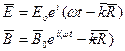
То есть мы ищем решение уравнения Максвелла в виде плоских монохроматических волн.
Подставим решение в уравнение Максвелла при этом учтём, что оператор  можно заменить на
можно заменить на 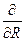
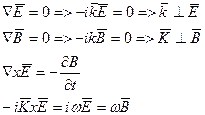
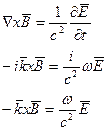

 2014-02-04
2014-02-04 3054
3054
