2014-02-02
789
Выборочный коэффициент эксцесса
Выборочный коэффициент асимметрии
Выборочное стандартное отклонение
Выборочная дисперсия
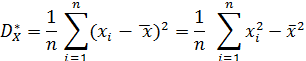
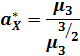
Выборочный центральный момент к-го порядка );
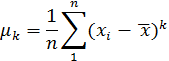
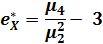
Предположим, что вид распределения генеральной совокупности известен (нормальное, экспоненциальное и т.п.). Тогда задача статистики сводится к оцениванию параметров этого распределения по результатам выборочных данных, в частности, к оцениванию математического ожидания, дисперсии и т.д.
•Точечной оценкой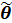 
неизвестного параметра θ называется приближенное значение этого параметра, найденное по выборочным данным:
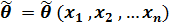
• Точечная оценка должна быть, по возможности, состоятельной, несмещенной и эффективной.
Состоятельной называется оценка, которая при увеличении объема выборки сходится по вероятности к оцениваемому параметру. Можно показать, что оценка является состоятельной, если при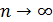 
выполняются соотношения
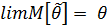
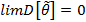
•Оценка называется несмещенной, если ее математическое ожидание совпадает с оцениваемым параметром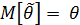
• Эффективной называется оценка, имеющая при заданном объеме выборки минимальную дисперсию.
