Рассмотрим наиболее распространенные в статистических методах обеспечения качества выборочные характеристики, являющиеся приближенной оценкой характеристик генеральной совокупности случайной величины. Ранее уже отмечалось, что характеристикой положения является математическое ожидание случайной величины, а характеристиками рассеяния - дисперсия или стандартное отклонение.
Математическое ожидание играет роль характеристики положения случайной величины в генеральной совокупности, и поэтому его иногда называют генеральным средним арифметическим значением случайной величины.
Если элементы генеральной совокупности независимы и распределены одинаково с математическим ожиданием М(Х) и дисперсией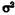 , то несмещенной оценкой для математического ожидания служит выборочное среднее арифметическое X, определяемое соотношением Заметим, что несмещенная оценка-это оценка, математическое ожидание которой равно значению оцениваемого параметра.
, то несмещенной оценкой для математического ожидания служит выборочное среднее арифметическое X, определяемое соотношением Заметим, что несмещенная оценка-это оценка, математическое ожидание которой равно значению оцениваемого параметра.
Математическое ожидание - величина постоянная для данной генеральной совокупности, а выборочное среднее арифметическое, получаемое в каждой конкретной выборке, всегда содержит элемент случайности, оно колеблется вокруг М(Х). Причем степень близости выборочного среднего арифметического к математическому ожиданию зависит только от объема выборки п и не зависит от отношения объема выборки к объему генеральной совокупности.
При большом количестве наблюдений (выборка большого объема или несколько выборок меньшего объема) выборочное среднее арифметическое или среднее арифметическое выборочных средних арифметических приближается к математическому ожиданию.
Таким образом, выборочное среднее арифметическое на практике используется в качестве приближенного значения математического ожидания. При этом следует иметь в виду, что выборочное среднее арифметическое значение X является случайной величиной и его разброс в квадрате, как это следует из центральной предельной теоремы, в n раз меньше, чем квадрат разброса значений xt контролируемого параметра, т.е.
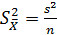 (1)
(1)
Здесь уместно отметить, что если генеральная совокупность распределена по нормальному закону, то распределение выборочных средних арифметических будет так же нормальным. Даже в том случае, когда генеральная совокупность имеет другой закон распределения, распределение выборочных средних будет приближаться к нормальному, и это приближение будет тем лучше, чем больше объем выборок.
Если математическое ожидание М(Х) генеральной совокупности известно, то дисперсия генеральной совокупности определяется выражением
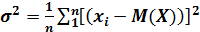 (2)
(2)
Однако на практике математическое ожидание генеральной совокупности, как правило, неизвестно, несмещенную оценку дисперсии генеральной совокупности приближенно определяют с использованием выражений для выборочной дисперсии
Вместе с тем выборочное стандартное отклонение может служить лишь смещенной оценкой стандартного отклонения генеральной совокупности. Заметим, что смещение оценки - это разность между математическим ожиданием оценки и оцениваемым параметром.
В случае выборки большого объема число (n-1) относительно мало отличается от n и поэтому для несмещенной оценки дисперсии генеральной совокупности можно использовать следующее приближенное соотношение
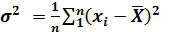 (3)
(3)
По теоретическим соображениям выражение (3) используется чаще, чем выражение (2). Однако для выборок большого объема оба эти выражения дают практически одинаковые результаты, и только при малых значениях объема выборки различие между этими выражениями весьма заметно
Ошибки репрезентативности могут быть рассчитаны как средняя или стандартная (μ) и максимальная с определенной вероятностью – предельная ( ).
).
Средняя ошибка выборки для собственно случайного и механического способа.
При повторном методе отбора 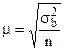 .
.
При бесповторном методе отбора 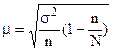 ,
,
где 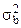 - дисперсия выборочных данных; n – объем выборки; N – объем генеральной совокупности.
- дисперсия выборочных данных; n – объем выборки; N – объем генеральной совокупности.
Средняя ошибка типического отбора.
При повторном методе отбора 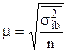 .
.
При бесповторном методе отбора 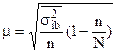 ,
,
где 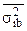 - средняя из групповых вариаций в выборке по типическим группам.
- средняя из групповых вариаций в выборке по типическим группам.
Средняя ошибка при отборе сериями (серийная выборка).
При повторном отборе 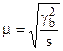 .
.
При бесповторном отборе 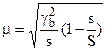 ,
,
где  - межгрупповая вариация; s – количество отобранных серий; S – количество серий в генеральной совокупности.
- межгрупповая вариация; s – количество отобранных серий; S – количество серий в генеральной совокупности.
Предельная ошибка выборки ( ) связана со средней ошибкой и коэффициентом доверия (t)
) связана со средней ошибкой и коэффициентом доверия (t)
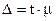 .
.
Коэффициент доверия зависит от вероятности, с которой можно гарантировать определенные размеры предельной ошибки:
Таблица – Критерий Стьюдента
| Коэффициент доверия (t) | |||
| Вероятность F(t) | 0,683 | 0,954 | 0,997 |
Обобщающая характеристика в генеральной совокупности (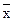 ) определяется доверительным интервалом, уточнение обобщающей характеристики выборочной совокупности (
) определяется доверительным интервалом, уточнение обобщающей характеристики выборочной совокупности (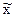 ) на предельную ошибку выборки:
) на предельную ошибку выборки:
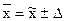 или
или  с заданной вероятностью.
с заданной вероятностью.
Приведенные выше формулы ошибок выборки позволяют заранее рассчитать тот объем выборки (репрезентативная выборка), при котором отклонение выборочных показателей от генеральных не превысит заданных размеров, гарантируемых с определенной вероятностью.
При повторном отборе 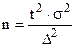 .
.
При бесповторном отборе 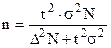 .
.
При определении необходимой численности выборки для определения дисперсии используют данные предыдущих обследований. При полном отсутствии каких-либо данных о вариации задают максимальную величину дисперсии: для количественного признака
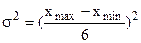 .
.
Для альтернативного признака  .
.
Малой выборкой называют выборку, объем которой не превышает 20 единиц (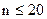 ).
).
Средняя ошибка малой выборки (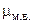 ) определяется по формуле
) определяется по формуле
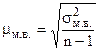 .
.
Для увязки средней и предельной ошибок малой выборки используется коэффициент распределения Стьюдента (псевдоним В. Госсета)
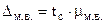 ,
,
где 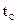 - коэффициент Стьюдента, определяемый по распределению Стьюдента
- коэффициент Стьюдента, определяемый по распределению Стьюдента 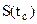 в зависимости от n.
в зависимости от n.
Вероятность того, что характеристика генеральной совокупности не выйдет за пределы 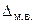 , с распределением Стьюдента связана следующим образом:
, с распределением Стьюдента связана следующим образом:
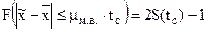 .
.
Последняя формула применяется для нахождения пределов генеральной средней с заданной вероятностью.
Выборочные данные представляют в табличной или графической форме
Основные правила записи результатов выборки:
-результаты хi записываются в порядке их регистрации,
- n- объем выборки.
Вариационный ряд составляют из величин хi,записанных в порядке возрастания. В ряду. х1= хmin, а хn = хmax.
Размах выборки R = хmax- хmin = хn- х1
При достаточно большом объеме выборки данные группируют, т.е. распределяют на интервалы одинаковой длины. Количество интервалов k определяют, исходя из величины выборки. Обычно от 8 до 20 интервалов. Иногда используется эмпирическая формула
k=1+3,32lg n
Ширина интервала ω = R/k
Количество nt элементов выборки, попавших в i-й интервал (i=1,2,… k), называется частотой. Результаты расчета сводят в таблицу частот, в которой показывают границы интервалов, середины zi каждого интервала, частоты ni, относительные частоты ni/n, накопленные относительные частоты 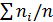 а также относительныe частоты, деленные на длину интервала ni/ωn.
а также относительныe частоты, деленные на длину интервала ni/ωn.
Выборочным распределением называется распределение дискретной случайной величины, принимающей значения х1 х2 …хn с вероятностями 1/n. График выборочной функции распределения (рис.1)/строится по значениям накопленных относительных частот. Можно показать, что при большом объеме выборки выборочная функция распределения является приближенной оценкой функции распределения F(x)генеральной совокупности.
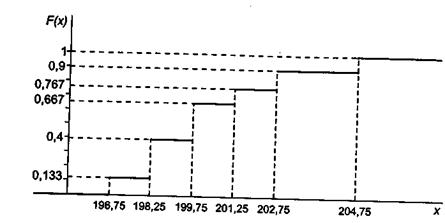
Рисунок 1 – График выборочной функции распределения
Гистограмма частот строится по значениям ni/ωn и •является приближенной оценкой плотности распределения f(x) генеральной совокупности.
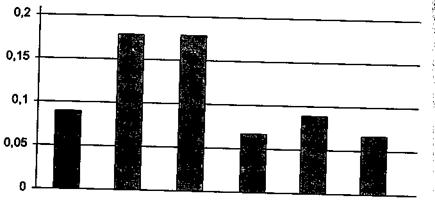
Рисунок 2 – Гистограмма частот
Числовые характеристики выборочного распределения определяются по аналогии с числовыми характеристиками дискретной случайной величины) с учетом того, что вероятности p=1/n/
Выборочное среднее (математическое ожидание выборки )
;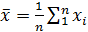
Выборочная мода Mo — элемент выборки, встречающийся с наибольшей частотой (для унимодального — одновершинного распределения)
Выборочная медиана Me — число, которое делит вариационный ряд на две части, содержащие одинаковое количество элементов
 2014-02-02
2014-02-02 835
835








