• Предположим, что случайная величина X на генеральной совокупности имеет математическое ожидание т и дисперсию σ2. В качестве точечной оценки математического ожидания можно принять выборочное среднее:
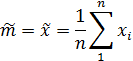
•Эта оценка является состоятельной и несмещенной. Действительно,
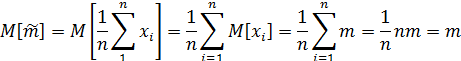
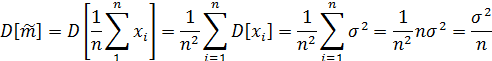
При 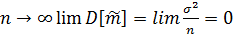
Если же выборка взята из нормально распределенной генеральной совокупности, то оценка является и эффективной.
При обосновании состоятельности оценки мы получили важную формулу для дисперсии выборочного среднего, которая будет использована в дальнейшем
: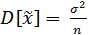
В качестве точенной оценки дисперси и 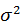
 генеральной совокупности принимается специальная характеристика, называемая несмещенной дисперсией:
генеральной совокупности принимается специальная характеристика, называемая несмещенной дисперсией:
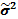 =
= 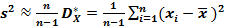
Одним из наиболее распространенных методов оценивания параметров распределения является метод максимального правдоподобия. Для непрерывной случайной величины с известной плотностью f(x,θ), зависящей от некоторого неизвестного параметра θ, вводится функция правдоподобия
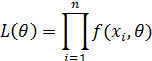
где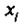 — фиксированные выборочные данные.
— фиксированные выборочные данные.
В качестве оценки параметра θ принимается такое значение, которое обеспечивает максимум функции правдоподобия. На практике, как правило, используется lnL(θ)— логарифмическая функция правдоподобия. Приравнивая нулю производную
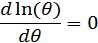
находят оценку максимального правдоподобия.
Иногда в статистических расчетах важно не только найти оценку параметра, но и охарактеризовать ее точность. Для этого вводится понятие об интервальной оценке параметра.
Доверительным интервалом параметра θ называется интервал (θ1 θ2 ) содержащий истинное значение θ с заданной вероятностью p=1-α
P(θ1<θ<θ2) = 1-α.
Число р называется доверительной вероятностью, или надежностью оценки, и принимается близким к единице: 0,9; 0,95; 0,99. Значение α называется уровнем значимости. Для доверительного интервала математического ожидания нормально распределенной генеральной совокупности при известной дисперсии σ2 можно получить следующее соотношение:
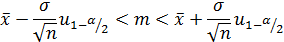
где u1-α/2 — квантиль нормального распределения порядка 1-α/2, определяемая по таблице
При неизвестной дисперсии генеральной совокупности формула для доверительного интервала математического ожидания нормально распределенной совокупности примет вид:
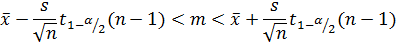
где s — квадратный корень из несмещенной дисперсии;
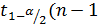 — квантиль распределения Стьюдента с степенью свободы (n-1) порядка 1-α/2, определяемая по таблице
— квантиль распределения Стьюдента с степенью свободы (n-1) порядка 1-α/2, определяемая по таблице
По аналогии может быть получена формула для расчета доверительного интервала дисперсии нормально распределенной генеральной совокупности при неизвестном математическом ожидании:
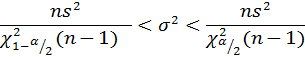
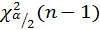 - квантиль распределения хи-квадрат с (n-1) степенью свободы порядка α/2, определяемая по таблице.
- квантиль распределения хи-квадрат с (n-1) степенью свободы порядка α/2, определяемая по таблице.
Рассмотрим пример
 2014-02-02
2014-02-02 1800
1800








