Решение. Найти 95%-й доверительный интервал для математической ожидания твердости сплава (в условных единицах)

Пример

Найти 95%-й доверительный интервал для математической ожидания твердости сплава (в условных единицах), если по результатам измерений получены следующие значения: 14,2; 14,8 14,0; 14,7; 13,9; 14,8; 15,1; 15,0; 14,5.

Объем выборки n = 9.

Выборочное среднее:

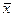= (14,2 + 14,8 +... + 14,5) / 9 = 14,56;

выборочная дисперсия:

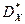= (14,2² + 14,8² +... + 14,5²) / 9 - 14.56² = 0,17;

несмещенная дисперсия:

s² = 9(0,17)/8 = 0,19; s =0,43;

доверительная вероятность

:p = 0,95;

уровень значимости α =0,05;1- α/2 = 0.975

квантиль распределения Стьюдента:t_0,975(8) = 2,306 (по таблице).

Тогда из выражения:

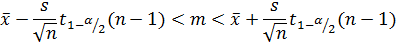
14,56 - 0,33<m< 14,56 + 0,33.

С вероятностью 0,95 математическое ожидание твердости сплава лежит в пределах от 14,23 до 14,89.