Понятие о спектрах

Совокупности коэффициентов a_k,b_k разложения периодической функции f(t) в ряд Фурье называют частотными спектрами этой функции.

Из формул (8) и (9) видно, что a_k= a_k(k); b_k= b_k(k), если f(t) имеет период 2π, а если период Т, то a_k= a_k(k∆ω); b_k= b_k(k∆ω). Здесь частота первой гармоники ∆ω=2π/T, т.е. спектры являются функциями, зависящими от номера гармоники k, как независящей переменной. Графически частотные спектры изображают в виде отрезков длины a_k,b_k, проведённых перпендикулярно к оси, на которую наносим значения k или k∆ω. Т.к. k=1,2,… частотные спектры имеют дискретный (разрывный) характер, расстояние между отдельными линиями спектра в общем случае равно ∆ω, а при t=2π – единице.

Совокупность комплексных чисел С_k=2с_k, определяемых для f(t) c периодом Т формулой (19) называется комплексным амплитудным частотным спектром.

Совокупность величин A_k= A_k(k∆ω) и φ_k=φ_k(k∆ω) (k=1,2,3…) называются соответственно амплитудным и фазовым частотными спектрами периодической функции f(t).

Ранее отмечалось, что k может быть как положительным, так и отрицательным. Поэтому график спектров А_k и φ_k имеет смысл и при положительных, и при отрицательных частотах ω=k∆ω

А_k=2│с_k│,

φ_k= -arg с_k=arctg (b_k/a_k).

Отсюда получим, что A_+│k│= A _-│k│, φ_+│k│= -φ _-│k│,

т.е. амплитудный частотный спектр является четно-симметричной, а фазовый частотный спектр – нечетно-симметричной функцией частоты ω. Таким образом, при определении спектров часто достаточно изобразить лишь половину спектра при k∆ω > 0.

Пример. Изобразить частотные спектры периодической функции

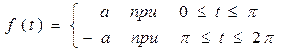
Заданная функция имеет значения коэф.(см. пред. пр.) a_k=0; b_k=0 при четном k; b_k=4a/(πk) – при нечетном k.

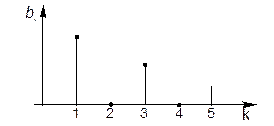
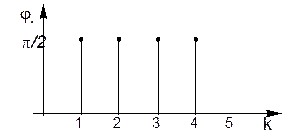
Отметим, что между периодическими функциями и их частотными спектрами существует взаимнооднозначное соответствие: f(t) определяет ее частотные спектры и, наоборот, зная частотные спектры, можно указать какой периодической функции они принадлежат. Благодаря этому соответствию в ряде задач техники оказывается удобным операции над периодическими процессами заменять операциями над частотными спектрами, характеризующими эти процессы.