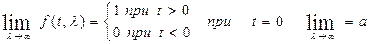
К категории особых функций относится дельта – функция Дирака, называется также импульсной функцией, первого порядка. Дельта функция определяется равенством:
 , причем
, причем
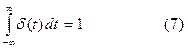
Условия (6) и(7) оказываются несовместимыми, если рассматривать их с позиций классического матанализа, и поэтому дельта – функция не является функцией в обычном смысле. Однако в классе обобщенных функций она занимает равноправное место.
Дельта–функция обычно рассматривается как предел последовательностей дельта - образных гладких (имеющих производные любого порядка) функций являющихся производными по t от (3). Например:
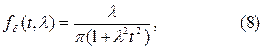
является дельта – образной последовательностью, т.к.
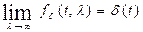
В самом деле, при t≠0
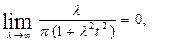
при t=0
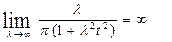 , причем
, причем
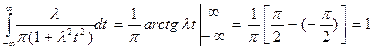
При таком определении дельта – функция является четной. Дельта – функция может апроксимироваться и разрывными функциями. Например, последовательность функций
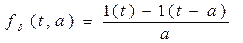 , характеризующих импульсы высотой 1/a и длительностью a, при a→0, сходятся к дельта функции, т.е.
, характеризующих импульсы высотой 1/a и длительностью a, при a→0, сходятся к дельта функции, т.е.
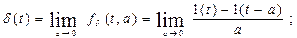
Смещенная единичная ступенчатая функция и дельта–функции определяются равенствами:
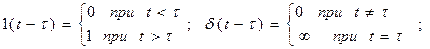
Рассмотрим важное свойство дельта – функции. Пусть f(t) непрерывна и ограниченна в интервале [-∞;∞]. Тогда справедливо равенство:
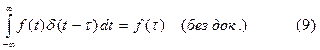
Это соотношение определяет так называемое “фильтрующее” или “выхватывающее” свойство дельта – функции.
Определим теперь спектральные характеристики 1(t). Единичная ступенчатая функция не удовлетворяет условию абсолютной интегрируемости, и поэтому преобразование Фурье для такой функции не существует. Однако, используя понятие дельта–функции, можно построить спектральную характеристику и для неё. Покажем, что её спектральная характеристика определяется равенством:
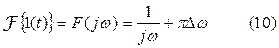
Подставляя F(jω) в формулу обратного преобразования Фурье и, учитывая фильтрующее свойство дельта–функции, получим
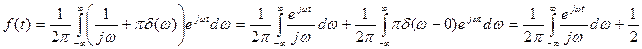
Учитывая Лемму Жордана и основанные на ней способы вычисления несобственных интегралов, найдём
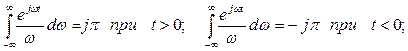
Следовательно:
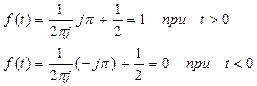
Таким образом, обратное преобразование Фурье функции F(jω) приводит к 1(t), и поэтому правая часть равенства (10) является её спектральной характеристикой.
Определим спектральную характеристику дельта–функции (6).
Применяя 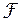 , получим учитывая фильтрующее свойство:
, получим учитывая фильтрующее свойство:
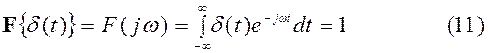
Спектральная характеристика смещенной дельта-функции будет
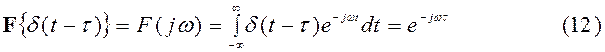
Из (11) и (12) следует, что модуль спектральной характеристики дельта-функции │F(jω) │ равен единице.
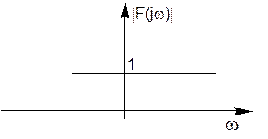
Отсюда следует, что амплитуды гармоник представления δ - функции в виде интеграла Фурье равны на всем диапазоне частот от -∞ до ∞.
Найдем спектральную характеристику суммы двух дельта-функций
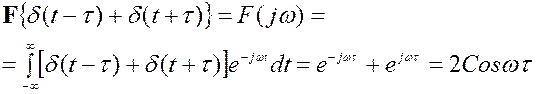
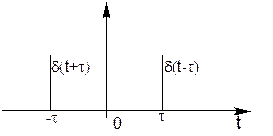
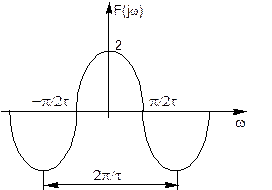
Пусть задана косинусоидная функция
f(t) = А1 Cos ω1 t
c амплитудой А1 и частотой ω1. Амплитудный спектр этой функции состоит из двух отрезков высотой А1 при частотах ω= ± ω1; для других значений частоты ω значения амплитудного спектра равны нулю.



Косинусоида не удовлетворяет условию абсолютной интегрируемости на интервале (-∞;∞) поэтому преобразование Фурье непосредственно не может быть использовано для определения спектральной характеристики (13). Покажем, что
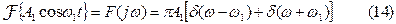
Для этого используем обратное преобразование Фурье
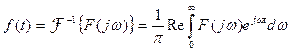 .
.
Подставляя в эту формулу выражение (14) получим
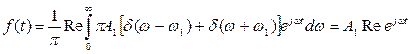
Здесь использовано фильтрующее свойство дельта-функции, причем точка ω=ω1, расположена внутри интервала (0, ∞), а δ(ω+ω1) = 0 при ω>0.
Следовательно, с учетом формулы Эйлера
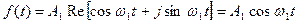
т.е. 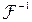 даём косинусоиду, следовательно
даём косинусоиду, следовательно
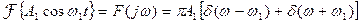
Пусть теперь задана периодическая функция
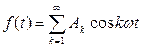
Ее спектральная характеристика.
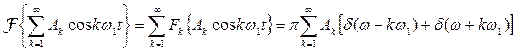
Если
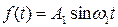
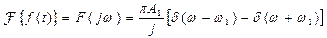 ,
,
её модуль
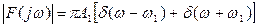
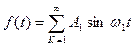
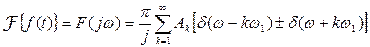
 2014-02-02
2014-02-02 1161
1161
