2014-02-02
12575
Совокупность операций, позволяющих по заданной функции f(t) находить соответствующую ей спектральную характеристику F(iω) называется преобразованием Фурье:
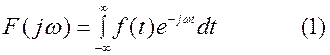
Символически формулу (1)будем записывать в виде
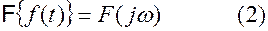
Интеграл в правой части (1) как и ранее понимается в смысле главного значения, т.е.
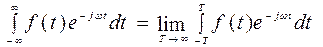
Равенство (1) устанавливает связь между функцией f(t), аргументом которой служит t, и ей соответствующей комплексной функцией F(iω), имеющей в качестве аргумента частоту ω.
Формула интеграла Фурье
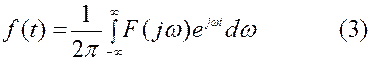
позволяет от известной функции F(iω) определить соответствующую ей функцию f(t). На этом основании формулу (3) называют обратным преобразованием Фурье. Символически будем записывать
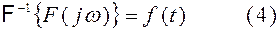
В ряде задач автоматического регулирования функция f(t) характеризует процесс, имеющий место лишь начиная с некоторого момента времени t, который можно принять за нулевой.
В этом случае f(t) ≡ 0 при t < 0 (1) принимает вид
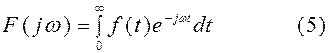
Преобразование (5) называется прямым односторонним преобразованием Фурье. Обратное преобразование Фурье, соответствующее прямому одностороннему преобразованию, остается двусторонним по переменной ω и дается равенством
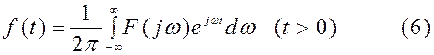
При t= 0, значение правой части (6) равно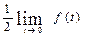 
;
при t < 0, f(t) ≡ 0
