Логарифмический критерий устойчивости

Широкое распространение критерий Найквиста получил при суждении об устойчивости по логарифмическим частотным характеристикам. Возможность такого суждения вытекает из того, что АФХ разомкнутой системы

W(j)=|W(j)|·e^{j arg W(j)}

Полностью определяется парой характеристик

L()=20 lg|W(j)| и j()=arg W(j)

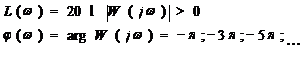Точками пересечения годографа W(j) с отрезком отрицательной вещественной оси (-¥,-1) соответствуют точки для которых.

Точки ЛФЧХ 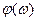, для которых L(w)>0 и в которых она пересекает при увеличении w прямые -p,-3p,… снизу вверх условимся называть отрицательными переходами П_-, а сверху вниз – положительными переходами П₊.

Тогда критерий устойчивости может быть сформулирован следующим образом. САР устойчива, если разность между положительными и отрицательными переходами ЛАЧХ равна l/2, где l – число корней характеристического уравнений разомкнутой системы, лежащих в правой полуплоскости. П₊-П_-=l/2

Для частного случая, когда l=0 (разомкнутая система устойчивая или нейтральна), получается, что система устойчива, если разность между

П₊ - П- = 0.

Если пересечение j(w) с осью -p происходит только один раз

П₊-П_- = -1¹0; l=0 – система неустойчивая

w_с>w_п

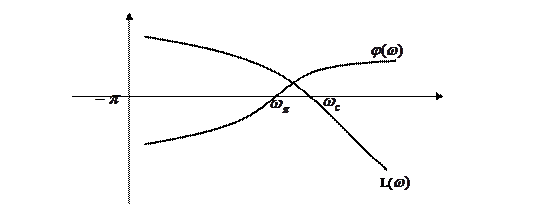
П₊-П_-=0-0-0; l=0 – замкнутая система устойчивая

w_с<w_п

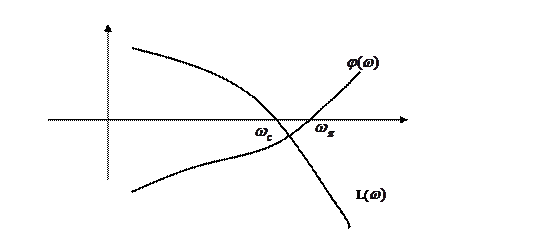
Замкнутая система будет устойчивая, когда L(w)=0 достигается раньше, чем j(w)= -p. Если w _с= w_п замкнутая система находится колебательной границе устойчивости.