Критерий устойчивости Михайлова

Предложен Михайловым (сов. ученый) в 1936 году. Позволяет судить об устойчивости замкнутой системы по виду кривой Михайлова, представляющей собой годограф вектора

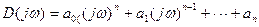
при изменении от 0 до ¥.

Годограф представляет собой характеристический полином замкнутой системы D(s) при s=j.

Выделив в правой части (1) вещественную и мнимую составляющие можно записать D(j)=U()+jV() где

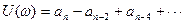(2)

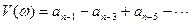
Кривая Михайлова строится в плоскости (U;jV) по точкам в соответствии с (2). Критерий Михайлова формулируется таким образом:

Для устойчивости линейной САР необходимо и достаточно, чтобы вектор D(j) при изменении от 0 до ¥ повернулся на угол Y_d=n·p/2 против часовой стрелки (в положительном направлении), где n-степень характеристического уравнения исследуемой системы.

D(s)=a₀(s-s₁)(s-s₂)..(s-s_n)

Где s₁ s₂... s_n – корни характеристического уравнения

Кривая Михайлова может быть описана уравнением

D(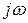)=a₀(j-s₁)(j-s₂)..(j-s_n).

Результирующий угол поворота вектора D(j) при изменении от 0 до ¥ обозначим через ,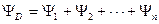

Где 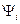(i=1..n) – составляющие угла поворота вектора D(j), определяемые сомножителями (j-s_i). Нетрудно видеть, что каждый сомножитель дает поворот радиуса вектора при изменении от 0 до ¥ на угол ±p/2 в случае вещественных корней и на угол ±(p/2±¡) для комплексного корня, где

¡ =arctg(b ¤ a) (s_i=±a ±jb). Паре комплексных корней соответствуют два сомножителя, поворачивающие радиус вектор на угол ±p. Положительные повороты (против часовой стрелки) имеют место при отрицательной вещественной части корня.

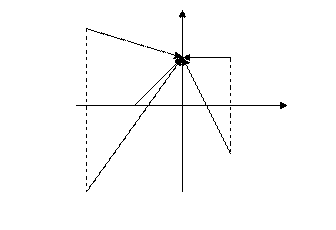Действительно, каждому множителю (j-s_i) можно поставить в соответствие вектор на плоскости корней, начало которого находится на точке s_i, а конец расположен на мнимой оси в точке j.

При изменении j от 0 до ¥ получаем указанные приращения аргумента.

Таким образом, если характеристическое уравнение замкнутой системы будет иметь l₃ корней с положительными вещественными частями, то каковы бы ни были эти корни (вещественные или мнимые), им будет соответствовать сумма углов поворота, равная

-l₃ ·p/2

Остальным (n-l₃) корням, имеющим отрицательные вещественные части, будет соответствовать сумма углов поворота, равная

(n- l₃) ·p/2. Следовательно, результирующий угол поворота вектора D(j) при изменении от 0 до ¥ Y_d=(n- l₃) ·p/2 - l₃·p/2 = p/2·n-pl₃

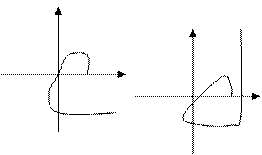
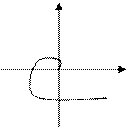
Для устойчивой САР кривая Михайлова должна проходить последовательно n квадрантов. Кривая начинается на вещественной полуоси (при =0; D(j0)=a_n) при ®¥ D(j)®¥. Если система находится на апериодической границе устойчивости, то a_n=0 и кривая идет из начала координат. При колебательной границе устойчивости кривая проходит через начало координат. Кривая соответствующая неустойчивой системе показана на последнем рисунке.