Этот критерий позволяет судить об устойчивости САР по виду ее АФХ в разомкнутом состоянии.
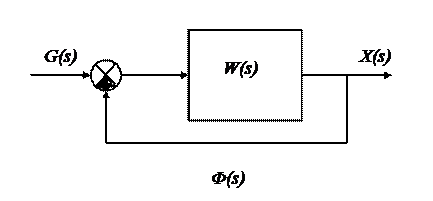
Передаточная функция замкнутой САР может быть выражена через передаточную функцию разомкнутой системы W(s).
Ф(s)=W(s)/(1+W(s))
Пусть W(s)=M(s)/Q(s), где M(s) и D(s) – многочлены от s, причем степень многочлена M(s) меньше степени многочлена Q(s). Передаточная функция замкнутой системы имеет вид:
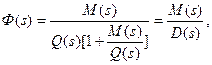
где 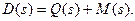
Многочлен D(s) является характеристическим многочленом замкнутой, а многочлен Q(s) – разомкнутой автоматической системы. Очевидно, что степени этих многочленов равны.
Образуем сумму
W1(j )=1+W(j
)=1+W(j )=1+M(j
)=1+M(j )/Q(j
)/Q(j )=D(j
)=D(j )/Q(j
)/Q(j )
)
Из критерия Михайлова следует, что замкнутая система будет устойчивой, если приращение аргумента Yd=n·p/2, где n -степень характеристического многочлена D(s); при этом условии D(s) не имеет корней в правой полуплоскости плоскости S.
В разомкнутом состоянии САР в общем случае может быть неустойчивой, то есть Q(s) может иметь корни в правой полуплоскости (полагаем, что на мнимой оси Q(s) корней не имеет). Если число таких корней равно L, то приращение аргумента (угол поворота вектора Q(j ) при изменении
) при изменении 
от 0 до ¥)
Yq=n·p/2-p·L
Следовательно, угол поворота вектора суммы W1(j ) при изменении
) при изменении  от 0 до ¥
от 0 до ¥
Y=Yd - Yq= n·p/2 - n·p/2-n·L=p L
Для устойчивой системы вектор W1(j ) при изменении
) при изменении  от 0 до ¥ повернется на угол pL в положительном направлении (против часовой стрелки) так как функция W(j
от 0 до ¥ повернется на угол pL в положительном направлении (против часовой стрелки) так как функция W(j ) отличается от W1(j
) отличается от W1(j ) на (-1), то для устойчивой замкнутой системы вектор W(j
) на (-1), то для устойчивой замкнутой системы вектор W(j ) при изменении
) при изменении  oт 0 до ¥ повернется на угол pL относительно точки (-1, j0), иными словами АФХ разомкнутой системы должна охватывать L/2 раз точку (-1, j0).
oт 0 до ¥ повернется на угол pL относительно точки (-1, j0), иными словами АФХ разомкнутой системы должна охватывать L/2 раз точку (-1, j0).
На основании выше изложенного, критерий Найквиста может быть сформулирован следующим образом:
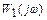
-1;j0 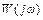
Автоматическая система, устойчивая в разомкнутом состоянии, будет устойчива в замкнутом состоянии, если АФХ разомкнутой системы W(j ) не охватывает точку (-1,j0). Если система в разомкнутом состоянии неустойчива и ее характеристический многочлен имеет L корней в правой полуплоскости, то для устойчивости автоматической системы в замкнутом состоянии необходимо и достаточно, чтобы АФХ W(j
) не охватывает точку (-1,j0). Если система в разомкнутом состоянии неустойчива и ее характеристический многочлен имеет L корней в правой полуплоскости, то для устойчивости автоматической системы в замкнутом состоянии необходимо и достаточно, чтобы АФХ W(j ) охватывала точку (-1,j0) в положительном направлении L/2 раз.
) охватывала точку (-1,j0) в положительном направлении L/2 раз.
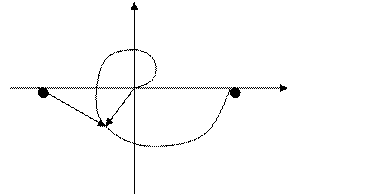
Примеры. Разомкнутая система неустойчива
L=1 y=p, охватывает ½ раз - система устойчива
П++П-= ½
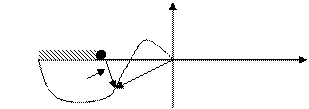
y=-p¹p, - система не устойчива
П++П-=½-1¹½ - не устойчива

L=2
y=2p, охватывает 1 раз L/2 – замкнутая система устойчива
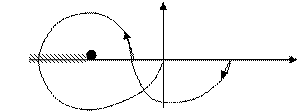
П+-П -= 1 – устойчива.
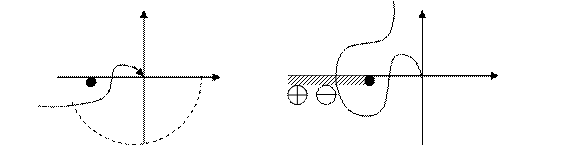
Если АФХ имеет сложную форму, то определение результирующего поворота (охвата) сложно. В этом случае удобно использовать правило переходов.
Переход АФХ W(jw) через участок вещественной оси (-¥,-1) с возрастанием частоты называется положительным если он проходит “сверху”-”вниз” и отрицательным, если “снизу”-”вверх”. Обозначают + и – в кружочках. Если АФХ начинается на вещественной оси в интервале (-¥;-1), то эта точка считается за + ½ перехода, если вниз, и за - ½, если вверх.
Если разомкнутая система является неустойчивой, то для устойчивости замкнутой системы необходимо и достаточно, чтобы разность между общим числом П+ - положительных и П -- отрицательных переходов АФХ W(j ) через участок вещественной оси (-¥;-1) при изменении частоты от 0 до ¥ было равно L/2, где L –число правых корней характеристического уравнения системы.
) через участок вещественной оси (-¥;-1) при изменении частоты от 0 до ¥ было равно L/2, где L –число правых корней характеристического уравнения системы.
П+ -П - =L/2
Разомкнутая система – устойчива
L=0
y=0
П+-П -=0
устойчива замкнутая система
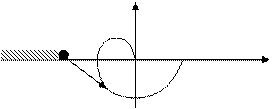
y=0
П+-П-=0 замкнутая система устойчива
не охватывает
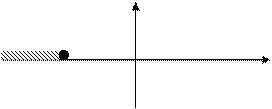
 |
y=2p;¹0
П+-П-= -1¹0 замкнутая система не устойчива
охватывает


 |
Если АФХ проходит через (-1;j0) то замкнутая система находится на колебательной границе устойчивости.
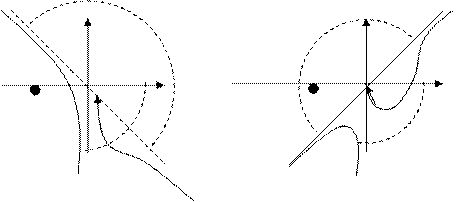
Некоторые особенности применения критерия Найквиста появляются при исследовании устойчивости систем, нейтральных в разомкнутом состоянии. Это системы имеющие нулевые корни (апериодическая граница устойчивости), а также системы, находящиеся в разомкнутом состоянии, на колебательной границе устойчивости, то есть имеющих чисто мнимые корни.
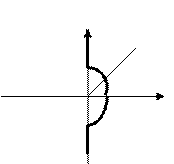 Например, если Q(s) имеет один нулевой корень, то годограф W(j
Например, если Q(s) имеет один нулевой корень, то годограф W(j ) при
) при  ®0 обращается в бесконечность.
®0 обращается в бесконечность.
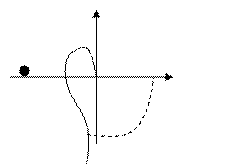 | |||
 | |||
В этом случае для сохранения формулировки критерия, справедливой для устойчивых в разомкнутом состоянии систем, включают нулевой корень в левую полуплоскость, огибая его справа окружностью бесконечно малого радиуса r®0. При этом годограф W(j ) дополняется частью окружности бесконечно большого радиуса, проводимой по часовой стрелке от положительной полуоси, то есть на угол p/2.
) дополняется частью окружности бесконечно большого радиуса, проводимой по часовой стрелке от положительной полуоси, то есть на угол p/2.
 При нескольких нулевых корнях, угол дополнения АФХ окружностью бесконечно малого радиуса yдоп=¡p/2 где ¡- число нулевых корней (порядок астатизма)
При нескольких нулевых корнях, угол дополнения АФХ окружностью бесконечно малого радиуса yдоп=¡p/2 где ¡- число нулевых корней (порядок астатизма)
Аналогичные дополнения приходится проводить при наличии чисто мнимых корней в характеристическом уравнении разомкнутой системы, так как в этом случае АФХ имеют разрывы
 |
 2014-02-02
2014-02-02 561
561








