Критерий устойчивости Рауса-Гурвица

Критерий устойчивости Рауса-Гурвица относится к алгебраическим критериям устойчивости, накладывающим ограничения на коэффициенты характеристического уравнения. Процессор математики Кембриджского университета Раус в 1875 году сформулировал условия устойчивости в виде таблицы. Швейцарский математик Гурвиц в 1895 году опубликовал критерий устойчивости в виде системы определений. Оба дают одни и те же алгебраические неравенства и отличаются только способами их получения. Рассмотрим этот критерий в форме Гурвица.

Если характеристическое уравнение системы имеет вид уравнения (2), причем a₀>0, то для устойчивости линейной САР необходимо и достаточно, чтобы были положительными n определителей Гурвица – D₁,D₂...D_n.

Определители Гурвица представляют собой диагональные определители квадратной матрицы n-го порядка, составленной из коэффициентов (2), которая строится следующим образом:

По главной диагонали записываются коэффициенты а₁,а₂...а_n.

Вниз по столбцу от этих коэффициентов расположены коэффициенты с убывающими номерами, а вверх – с возрастающими. При этом полагается a_i=0, если i<0 или i>n. Такая матрица называется матрицей Гурвица Г.

; ; ; .

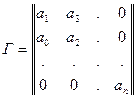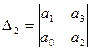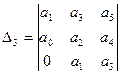Легко убедиться в том, что D_n=a_nD_n-1. Поэтому последний определитель Гурвица D_n вычислять не нужно, а условие 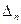>0 выполняется при a_n>0 и

D_n-1>0.

Условие, при котором САР находится на границе устойчивости можно получить, положив D_n=0 или a_nD_n-1=0.

Условие a_n=0, D_n-1¹0 – соответствует апериодической границе устойчивости.

Условие a_n¹0, D_n-1=0 – соответствует колебательной границе устойчивости.

Пример. Исследуем устойчивость простейшей следящей системы, в которую входит инерционный усилитель с постоянной времени T_y и исполнительный двигатель с постоянной времени T_м. Все остальные элементы системы считаются безинерционными.

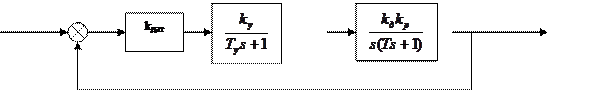
В этом случае передаточная функция разомкнутой системы

W(S)=K/(s(T_мs+1)(T_уs+1)),

где k=k_дат k_y k_д k_p, а передаточная функция замкнутой системы

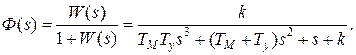
Характеристическое уравнение системы имеет вид

a₀s³+a₁s²+a₂s+a₃=0;

где a₀=Т_мТ_у; a₁= Т_м+Т_у; a₂=1; a₃=k

Условия устойчивости:

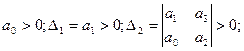или

Т_м>0; Т_y>0; Т_м+Т_y>k·Т_м·Т_{y ,} или .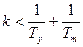

Система будет находиться на колебательной границе устойчивости, если 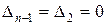, то есть

к_кр=1/Т_y+1/Т_м.

Полагая Т_м =const построим область устойчивости в пространстве параметров k и T_у,

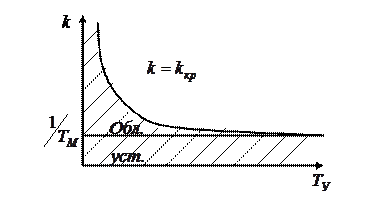
Видно, что увеличение постоянных времени T_у и T_м сужает область устойчивости, уменьшая верхнее значение коэффициента k.