Запас устойчивости замкнутой системы определяется степенью удаления АФХ разомкнутой системы W(jw) от точки (-1;j0). Прохождение АФХ через эту точку соответствует нахождению САР на колебательной границе устойчивости. Удаление АФХ от (-1;j0) соответствует повышению запаса устойчивости.
Рассмотрим количественные оценки степени удаления АФХ W(jw) от точки (-1;j0). Удалённость можно характеризовать при помощи двух положительных чисел Hm и gср, называемых запасами устойчивости системы по амплитуде (по модулю) и по фазе.

jV
 Hm1
Hm1


 Hm2
Hm2
 |




 -1
-1
wp1 wp2 U
wср gср
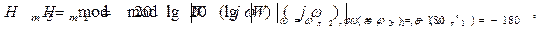
Из рис. следует, что
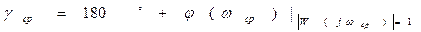 |
Запас устойчивости по амплитуде показывает, на какую величину должен измениться модуль АФХ разомкнутой системы на частоте, при которой фазовая характеристика достигает значения (-180°), для того чтобы замкнутая САР оказалась на колебательной границе устойчивости.
Запас устойчивости по фазе gср показывает, на какую величину должно увеличиться отставание по фазе в разомкнутой системе на частоте, при которой АЧХ равняется единице (т.е. ½W(jwср)½=1) для того, чтобы замкнутая САР оказалась на колебательной границе устойчивости.
Оценки Hm и gср просты, наглядны и удобны. Ими легко пользоваться также в тех случаях, когда рассматриваются логарифмические частотные характеристики разомкнутой системы.
 j(w) L(w)
j(w) L(w)
 L(w)
L(w)
j(w)


 -180° wср wп
-180° wср wп
Hm w
-90° gср
Достаточными запасами устойчивости считаются: Hm ³ 6-12дб, gср ³ 30°.
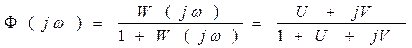 |
Для оценки степени удалённости АФХ разомкнутой системы от точки
(-1;j0) может применяться показатель колебательности М. Величину М легко определить по АФХ разомкнутой системы:
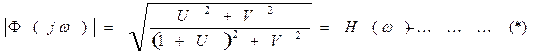 |
При H(w)=H=const выражение определяет в неявном виде некоторую функциональную зависимость между U и V. Геометрически на плоскости (U,jV) эта зависимость сводится к кривой, представляющей собой геометрическое место всевозможных значений U и V, при которых АЧХ замкнутой системы имеет постоянное значение H. Для каждого значения H (*) определяет свою кривую на плоскости (U;jV). Найдём уравнение семейства кривых H=const. Для этого возведём обе части (*) в квадрат и преобразуем его.
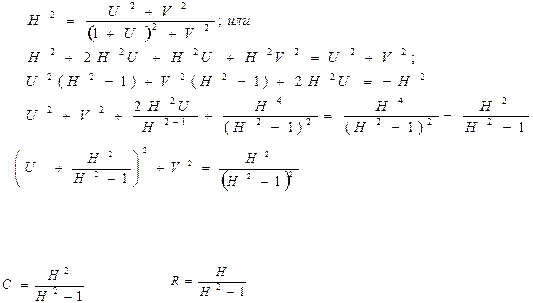 |

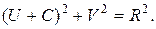
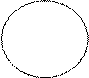
Это окружность с радиусом R и центром (-С). При H=1 C=R=¥ и окружность вырождается в прямую, параллельную jV и проходящую слева от неё на расстоянии 0,5.
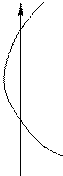 |
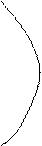 jV
jV

 1,2 H=1 H=8
1,2 H=1 H=8
 1,6 0,6
1,6 0,6

 1,8
1,8
 H=0,4
H=0,4





 3 -1
3 -1
wmax U
 | |||||
 | |||||
 |
W(jw)
Окружности соответствующие H>1 слева, а H<1 справа от прямой H=1. При H®¥ окружность вырождается в точку с координатами (-1;j0).
По семейству окружностей H=const и АФХ разомкнутой системы не трудно построить АЧХ H( )=
)=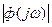 .Для каждого значения частоты
.Для каждого значения частоты  на АФХ
на АФХ 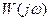 амплитудная характеристика
амплитудная характеристика 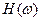 равна индексу той окружности H=const,которая проходит через точку АФХ соответствующую рассматриваемому значению w.
равна индексу той окружности H=const,которая проходит через точку АФХ соответствующую рассматриваемому значению w.
Наибольшее значение Hmax АЧХ H(w) равно индексу той окружности H=const, которой касается АФХ разомкнутой системы. На рис. Hmax=3. wmax=wр и равны значению w при котором происходит касание.
По значению Hmax легко определить показатель колебетельности М. Так для астатических систем M=Hmax, т.е. показатель колебательности равен индексу той линии, которой касается W(jw).
В связи с этим для астатических систем линии H=const части условно называют линиями постоянных значений показателя колебательности М и оцифровку дают прямо в значениях М.
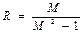 |
Для астатических систем величина показателя колебательности не превосходит заданного значения М, если АФХ разомкнутой системы не заходит внутрь запретной зоны, представляющей собой круг радиуса:
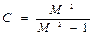 |
с центром в точке
на отрицательной вещественной полуоси.

 M/(M-1) jV
M/(M-1) jV


 C=M2/(M2-1)
C=M2/(M2-1)

 M/(M+1)
M/(M+1)




 -1 w=¥ U
-1 w=¥ U
 D A g
D A g
B
Запретная зона окружает точку (-1;j0) и обеспечивает получение необходимого запаса устойчивости. Показатель колебательности может быть определён и в случае использования логарифмических частотных характеристик. Для этого предварительно рассмотрим условия, которые должны удовлетворять отдельно ЛАЧХ и ЛФХ для 
того, чтобы W(jw) не попала в запретную зону. На окружности (см. рис.) возьмём произвольную точку В и проведём в неё вектор. Из треугольника ОВД для этого вектора найдём связь между модулем А и запасом по фазе g.
По теореме косинусов: 
Так как
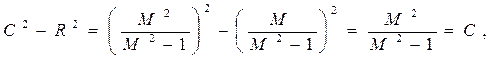
то 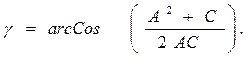 (**)
(**)
 2014-02-02
2014-02-02 918
918








