С учетом этих предположений построим ковариационную матрицу

Посчитаем дисперсию для нашего специфического примера, то есть сумму всех диагональных и недиагональных элементов матрицы.

δ_p² = N*1/N²var + (N² – N)*(1/N²)cov = 1/Nvar + (N² – N/N²)cov = 1/Nvar + (1-1/N)cov,

при N => ∞; 1/Nvar => 0, 1/N => 0. Следовательно

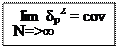Предел:

То есть получается, что дисперсия ушла, осталась только ковариация. Для примера о портфеле с множеством ценных бумаг.