Модель рынка товаров

Классическая макромодель экономического равновесия.

Классическая макроэкономическая модель рынка товаров, рынка труда и рынка ценных бумаг. Схема динамического взаимодействия рынка товаров, рынка труда и рынка ценных бумаг.

Содержание

_

Макромодели экономического равновесия

ЛЕКЦИЯ 8

1. Классическая макроэкономическая модель рынка товаров, рынка труда и рынка ценных бумаг. Схема динамического взаимодействия рынка товаров, рынка труда и рынка ценных бумаг......................................................................................................................................... 2

1.1. Классическая макромодель..................................................................................... 2

1.2. Модель рынка товаров............................................................................................ 5

1.3. Модель рынка рабочей силы................................................................................... 6

1.4. Модель рынка денег................................................................................................. 9

1.5. Классическая макроэкономическая модель взаимовлияния рынков рабочей силы, товаров и денег........................................................................................................................ 10

Источники…………………………………………………………………………………… 12

Основой классической макроэкономической модели является так называемый закон Сэя, который в общей форме сводится к утверждению, что предложение товаров создает спрос. Закон Сэя следует понимать в том смысле, что не может быть разрыва между спросом на товары и их предложением в масштабах всей экономики, хотя в пределах одного или нескольких секторов допускаются расхождения между ними.

Это положение становится оправданным, если принять два допущения:

во-первых, в рассматриваемой экономической системе каждый участник процесса производства действует не просто ради удовольствия проявлять активность, а с целью приобретения тех или иных благ;

во-вторых, осуществляется натуральный обмен, в результате которого продукты производства непосредственно обмениваются друг на друга (бартер).

Экономисты-классики не считали, однако, что присутствие денег в обмене существенно усложняет доказательство закона Сэя: они рассматривали деньги чисто техническим посредником, облегчающим процесс обмена.

Из закона Сэя следует, что условием равновесия на товарном рынке является равенство между национальным доходом Y и объемом национальных расходов Е:

(Предложение) Y = E (Спрос) (1)

Отметим, что объем национальных расходов Е представляет собой, по существу, спрос предпринимателей и населения на товары, которые можно подразделить на инвестиции I и потребительские товары С

Е = I + С. (2)

С другой стороны, национальный доход Y (в простейшем варианте модели) предназначен для потребления С и сбережений S, т.е.

Y = C + S, (3)

и, таким образом, национальный доход можно трактовать как предложение товаров.

Сопоставлял соотношения (1) - (3), получаем условие равновесия между спросом и предложением

(Спрос) I = S (Предложение) (4)

Это означает, что для обеспечения равновесия на рынке товаров требуется выполнение равенства объемов инвестиций и сбережений.

Как достигается это равновесие? Экономисты-классики полагали, что в конкурентной экономической системе существует механизм, способный автоматически приводить ее в состояние равновесия. Рассмотрим модель действия такого механизма в рамках классического подхода.

В основе модели установления равновесия лежат следующие две гипотезы.

Первая основана на том, что с ростом нормы процента люди получают стимул сберегать больше, т.е. объем сбережений - возрастающая функция (при прочих равных условиях) нормы процента:

S = S(r), S'(r) > 0. (5)

Обоснованием этой гипотезы служат, например, такие рассуждения: ни один разумный человек, намереваясь делать сбережения, не станет держать их в ликвидной форме, если он может получить с этих сбережений процент (путем покупки акций, облигаций и т.д.). Поэтому рост нормы процента побуждает людей увеличивать сбережения, что в математической форме выражается соотношениями (5). График функции сбережений Y = S(r) представлен на рис.1.

Вторая гипотеза основана на предположении о монотонно убывающей зависимости инвестиций от нормы процента:

I = I(r), I'(r) < 0. (6)

Обоснованием второй гипотезы служат такие рассуждения: предприниматели готовы предложить некоторую "премию" тому, кто предоставит в их распоряжение денежные средства, необходимые для капиталовложений. Если процент, из которого эти заемные средства предоставляются, меньше нормы прибыли, получаемой от данных капиталовложений, то для предпринимателя выгодно взять деньги взаймы и осуществить инвестиции. Если же процент превышает ожидаемую норму прибыли, то предприниматель в результате такой "деловой активности" получит лишь убытки; в этом случае он предпочтет не использовать заемные средства. График функции инвестиций I = I(r), также изображен на рис. 1.

Y=S(r)

Y

0 r₁ r_E r₂ r

Рис. 1. Изменение сбережений и капиталовложений в зависимости от нормы процента.

Рассмотрим рыночный механизм установления равновесия между сбережениями и капиталовложениями (инвестициями), используя рис. 1. Предположим, что норма процента меньше равновесной r_E например r= r₁ < r_E. Тогда капиталовложения превышают сбережения, и, таким образом, не все предприниматели, желающие платить r₁ процентов за заемные средства, найдут владельцев сбережений, которые готовы предложить им деньги взаймы.

Другими словами, спрос на заемные средства (т.е. желаемые капиталовложения I ) в этом случае превышает предложение (т.е. сбережения S ), вследствие чего часть предпринимателей, оказавшаяся без необходимых им средств, готова платить более высокий (по сравнению с r₁) процент за взятые в заем деньги. Поскольку и владельцы сбережений в этой ситуации предпочтут получить более высокий процент, то, как видим, при r₁ < r_E имеет место тенденция увеличения нормы процента.

Итак, при r₁ < r_E имеет место избыток спроса на инвестиции, вследствие чего норма процента растет:

dr > 0 при r₁ < r_E (7)

Если же норма процента превышает равновесный уровень (r = r₂ > r_E), то предложение заемных средств S превышает спрос на них (т.е. желаемые капиталовложения I), вследствие чего не все, кто намерен сберегать, найдут предпринимателей, готовых заплатить r₂ процентов. Лица, не нашедшие "партнеров", будут предлагать свои сбережения даже на менее выгодных условиях, т.е. при более низком проценте r < r_{2 .} Это означает, что в этом случае имеет место тенденция к снижению нормы процента, т.е.

dr< 0 при r > r_E (8)

Из приведенных рассуждений следует, что с течением времени нарушение условия r=r_E приведет к установлению равновесия за счет увеличения или уменьшения нормы процента.

Таким образом, движение нормы процента в условиях рынка свободной конкуренции может обеспечить равенство между сбережениями и инвестициями и, следовательно, между совокупным спросом Е = C + I и совокупным предложением У= C + S. Тем самым обоснована справедливость закона Сэя в случае, когда учитываются сбережения и инвестиции.

Описанный выше механизм установления равновесия между инвестициями и сбережениями позволяет построить формализованную модель, на основании которой можно получить не только равновесные значения переменных, но и их зависимости от времени.

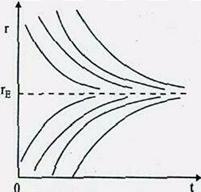
Рис. 2. Интегральные кривые дифференциального уравнения (9)

Действительно, из соотношений (7) и (8) следует, что для скорости изменения нормы процента можно принять

dr/dt = a(I(r) - S(r)), (9)

где а — коэффициент адаптации нормы процента (некоторая положительная константа, характеризующая реакцию рынка на несоответствие спроса предложению).

Дифференциальное уравнение (9) в силу монотонности функций I = I(r) и S = S(r ) имеет устойчивое равновесное решение r_E, которому соответствуют равные значения сбережений и капиталовложений. Это следует из того, что при r < r_E правая часть уравнения (9) положительна, а при r > r_E — отрицательна, вследствие чего любое отклонение от равновесного решения r = r_E приводит со временем к значению r = r_E. Интегральные кривые дифференциального уравнения (9) приведены на рис. 2.

Если зависимости I = I(r) и S = S(r ) линейны, то нетрудно получить аналитическое решение дифференциального уравнения (9). Пусть, например, функции капиталовложений и сбережений имеют вид

I = I_E – b(r-r_E),

S = I_E + c(r-r_E) (10)

соответственно, где b и с — положительные постоянные, I_E — равновесное значение инвестиций (I_E = S_E).

Подставляя соотношения (10) в уравнение (9), получим:

dr/dt = a(I_E – b(r-r_E)- I_E – c(r-r_E)) = -а(b+с(r-r_E),

откуда следует:

d(r-r_E)/(r-r_E)=-a(b+c)dt.

Интегрирование этого уравнения приводит к уравнению

1п(r-r_E)/(r₀--r_E) = - a(b+c)t, (11)

где r₀ — значение нормы процента при t = 0 (начальное значение).

Из соотношения (11) получаем окончательное выражение зависимости нормы процента от времени:

r= r_E + (r₀-r_E)ехр(-а(b+с)t). (12)

Как видим, решение (12) уравнения (9) при любом начальном значении r₀ асимптотически стремится к r _E при неограниченном росте t, что и означает установление в конце концов равновесия между капиталовложениями и сбережениями (рис. 2).

Теперь, после установления связи между сбережениями и капиталовложениями, можно построить в рамках классического подхода модель рынка товаров. Для этого необходимо принять еще одну гипотезу, согласно которой уровень производства Y = Y_E соответствует имеющимся производственным ресурсам. В силу принятого ранее допущения о неизменности объемов основных производственных фондов (поскольку все макропроцессы рассматриваются в краткосрочном периоде) примем, что объем выпуска товаров Y (национальный доход) зависит лишь от уровня занятости N:

Y = Y(N). (13)

Таким образом, если уровень занятости составляет N = N_E (при классическом подходе последний определяется в модели рынка рабочей силы), то в силу (13) уровень национального дохода (предложение) равен

y=y_e=y(n_e).

Этот доход распределяется на потребление С и сбережения S, причем за счет изменения нормы процента имеет место равенство между сбережениями и капиталовложениями. Знание объема сбережений s_e = i_e позволяет без труда определить и объем потребления:

c_e= y_e - s_e. (14)

При этом, согласно классическому подходу, дисбаланс между спросом (расходы) и предложением (доходы) в длительной перспективе невозможен, поскольку, в соответствии с законом Сэя, предложение формирует спрос.

Следовательно, математическая модель рынка товаров при классическом подходе содержит следующие уравнения:

y = y_e = y(n_e).

s_e = S(r_E) = I(r_E) (15)

c_e= y_e - s_e

первое из которых определяет уровень производства y_e по уровню занятости n_e, второе - равновесное значение нормы процента r_E и соответствующий ему уровень сбережений s_e, третье — уровень по­требления c_e.

Y

S IY_E=S_E+C_E