Метрические задачи

Лекция 10

Теорема Монжа.

Если две поверхности второго порядка одновременно описаны вокруг третьей поверхности второго порядка, то линия их пересечения распадается на две плоские кривые второго порядка.

Рис.52

На Рис.51 приведен комплексный чертеж двух пересекающихся конических поверхностей вращения (D и F), которые одновременно касаются третьей поверхности вращения (сферы). Линией их пересечения будут две плоские кривые (два эллипса m и n).

При прямоугольном проецировании Г.О. общего положения изображаются на плоскостях проекций с искажением их метрических характеристик.

Задачи, связанные с определением на чертежах длин отрезков, углов между прямыми и т.д. называются метрическими задачами. Любая метрическая задача на К.Ч. может быть решена с помощью двух основных (элементарных) метрических задач. Такими задачами являются следующие:

Первая основная метрическая задача (1 ОМЗ) – определить натуральную величину отрезка;

Вторая основная метрическая задача (2 ОМЗ) – перпендикулярность прямой и плоскости.

Рис.53

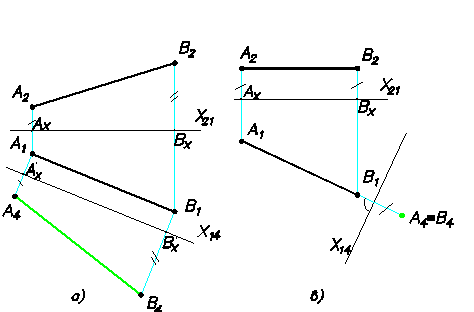
Пример. Определить натуральную величину отрезка АВ, заданного на комплексном чертеже [Рис.53, в)] двумя своими проекциями [ АВ (А 1 В 1, А 2 В 2 ) ].

Для начала рассмотрим иллюстрацию решения данной задачи, приведенную на однокартинном чертеже [Рис.53, а)]. Отрезок АВ (его натуральная величина) является гипотенузой прямоугольного треугольника АВВ*. Один из катетов (АВ*) этого треугольника равен горизонтальной проекции (А 1 В 1 ) отрезка АВ. Второй катет (ВВ*) является приращением аппликаты (Dz) отрезка АВ при переходе от точки А к точке В. Величину этого приращения легко определить на фронтальной проекции (А 2 В 2 ) отрезка АВ. Одновременно с определением натуральной величины отрезка АВ определим натуральную величину угла наклона прямой АВ к плоскости П 1(угол a).

Натуральная величина отрезка АВ, заданного на комплексном чертеже [Рис.53, в)] двумя своими проекциями А 1 В 1 и А 2 В 2,равна гипотенузе А 1 В* прямоугольного треугольника А 1 В 1 В*, один катет которого (А 1 В 1 ) равен проекции отрезка АВ на плоскости П 1, а второй катет равен приращению аппликаты (Dz) отрезка АВ (Dz = В 2 В*). Угол [Рис.53, в)] равен величине угла a наклона прямой АВ к плоскости П 1.

Определение натуральной величины отрезка АВ, заданного на комплексном чертеже [Рис.53, в)] двумя своими проекциями А 1 В 1 и А 2 В 2, можно выполнить и на фронтальной плоскости проекций П 2. При этом одновременно определим натуральную величину угла наклона прямой АВ к фронтальной плоскости проекций П 2. Угол в треугольнике между проекцией отрезка на данную плоскость и его натуральной величиной и есть угол между отрезком и данной плоскостью. (также см. Лекция 1, метрические свойства).

Вторая основная метрическая задача (2 ОМЗ)

(перпендикулярность прямой и плоскости)

Решение основано на признаке перпендикулярности прямой и плоскости.

Прямая, перпендикулярна к плоскости, если она одновременно перпендикулярна двум пересекающимся прямым, принадлежащим этой плоскости.

Пример. На комплексном чертеже (Рис.54) двумя своими проекциями (А 1 В 1 С 1 и А 2 В 2 С 2) задана плоскость S (АВС).

Задача. Построить проекции прямой n перпендикулярной плоскости S в точке А.

Решение. Через горизонтальную проекцию А 1точки А плоскости S проводим прямую n1 перпендикулярную горизонтальной проекции h 1 горизонтали h плоскости S. Также через фронтальную проекцию А 2 точки А плоскости S проводим прямую n2 перпендикулярную фронтальной проекции f 2 фронтали f плоскости S. На основании теоремы о прооецировании прямого угла (см. Лекция 1) делаем вывод, что прямая n ( n1, n2 ) одновременно перпендикулярна двум пересекающимся прямым (горизонтали h и фронтали f), принадлежащим плоскости S. Из этого вывода следует, что прямая n перпендикулярна плоскости S.