Раннее был рассмотрен предел числовой последовательности(функции натурального аргумента) 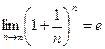 ("число е ")
("число е ")
Рассмотрим функцию 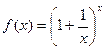 , которая отличается от числовой последовательности
, которая отличается от числовой последовательности 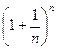 тем, что аргумент х "пробегает" все значения на числовой оси при
тем, что аргумент х "пробегает" все значения на числовой оси при 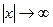 (не только натуральные).
(не только натуральные).
Найдем предел этой функции при 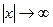 непосредственный подсчет предела приводит к выражению
непосредственный подсчет предела приводит к выражению 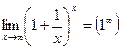 .
.
Но при вычислении 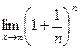 было показано что, этот предел
было показано что, этот предел 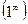 в действительности равен "числу е ". Рассмотрим случай, когда
в действительности равен "числу е ". Рассмотрим случай, когда 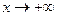 , очевидно, для
, очевидно, для 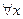
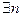 такое, что
такое, что 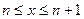 . Тогда
. Тогда 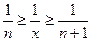 и
и 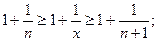
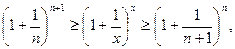
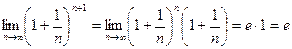 (теорема 5.4.4)
(теорема 5.4.4)
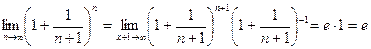 (теорема 5.4.4)
(теорема 5.4.4)
В таком случае 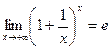 (теорема 5.4.2)
(теорема 5.4.2)
Можно сказать, что 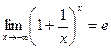 . Объединяя оба случая
. Объединяя оба случая 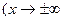 или
или 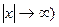 получаем:
получаем:
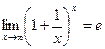 (5.4.7)
(5.4.7)
Этот предел называется вторым замечательным пределом. Положим 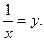 Если
Если 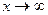 , то
, то 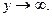 Получаем модификацию второго замечательного предела:
Получаем модификацию второго замечательного предела:
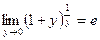 (5.4.8)
(5.4.8)
Второй замечательный предел позволяет раскрывать неопределенности вида 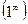 .
.
Примеры. Вычислить пределы.
1. 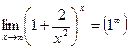 - неопределенность
- неопределенность
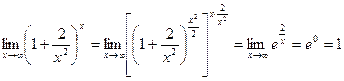
2. 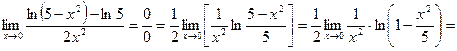
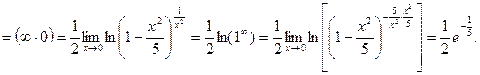
 2014-02-05
2014-02-05 567
567







