Зависимость между моментами инерции относительно

Для произвольного сечения, представленного на рис. 2.6, проведем центральные оси x, y, относительно которых S_х = Sу = 0, а затем параллельные им оси Х₁, У₁. Координаты центра тяжести в этих осях обозначим через 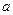и b, тогдакоординаты элементарной площадки dA будутх₁ =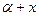, у₁ =.

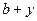Рассмотрим осевой момент инерции относительно оси Х₁:

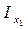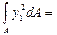
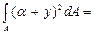
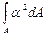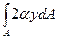= + +dA.

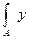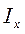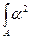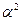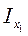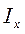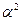Так как dA = S_х = 0, dA = , dA = А, то = + А,

Аналогично 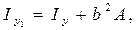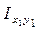═ 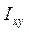+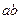А.

Таким образом, осевые моменты инерции относительно произвольных осей, параллельных центральным, находятся как сумма моментов инерции относительно центральных осей и произведения площади сечения на квадрат расстояния между осями, центробежный момент инерции – как сумма центробежного момента инерции относительно центральных осей и произведения площади сечения на расстояния между осями.