Рассмотрим геометрические характеристики прямоугольника, треугольника, круга и кольца.
Прямоугольник: выделим элементарную площадку dA ═ b·dy (рис.2.2). Тогда
І
х =
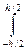
у
2 dA =
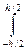
у
2 b dy = у
3 b ∕ 12|
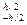
= bh
3 ∕ 12.
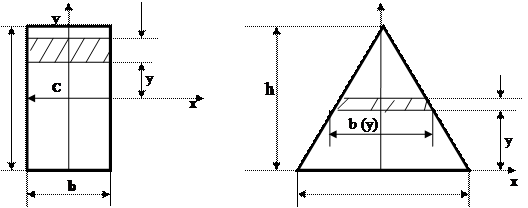
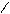

Треугольни к: элементарная площадка запишется выражением dA═b(у)·dy (рис.2.3). Из подобия треугольников следует b(у) ∕ b = (h─y) ∕ h, откуда получим
b(у) =b(1-  ), Іх =
), Іх = 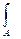 у2 dA =
у2 dA =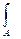 у2 b(1-
у2 b(1-  ) ·dy = b
) ·dy = b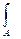 (у2 –
(у2 – 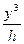 ) dy = b(
) dy = b(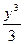 –
– 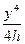 )|
)| = bh3 ∕ 12.
= bh3 ∕ 12.
Круг: выделим элементарную площадку dA (рис.2.4) в виде кольца с радиусами ρ и ρ+dρ, т.е., dA=2πρdρ.
Полярный момент инерции Іρ ═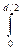 ρ2dA ═
ρ2dA ═ 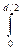 ρ22πρdρ ═
ρ22πρdρ ═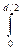 2πρ3dρ ═2πρ4 ∕ 4|
2πρ3dρ ═2πρ4 ∕ 4|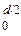 ═
═ 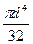
Так как Іρ = Іх + Iy,а для круга І х ═ Іy,тоІх═ Іy═  .
.
Кольцо: моменты инерции кольц а с диаметрами D и d (рис. 2.5)определятся как разница моментов инерции круга с диаметром D и круга с диаметром d
Іх = Іу =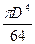 –
– 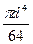 =
= 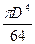 ( 1 -
( 1 - 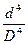 ).
).
Введем обозначение 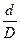 ═ α , тогда
═ α , тогда
Іх = Іу =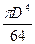 ( 1 – α4 ), І ρ=
( 1 – α4 ), І ρ=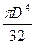 (1 – α4).
(1 – α4).
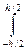 у2 dA =
у2 dA = 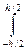 у2 b dy = у3 b ∕ 12|
у2 b dy = у3 b ∕ 12|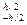 = bh3 ∕ 12.
= bh3 ∕ 12. 
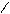

 ), Іх =
), Іх = 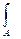 у2 dA =
у2 dA =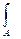 у2 b(1-
у2 b(1-  ) ·dy = b
) ·dy = b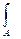 (у2 –
(у2 – 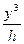 ) dy = b(
) dy = b(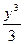 –
– 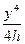 )|
)|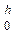 = bh3 ∕ 12.
= bh3 ∕ 12.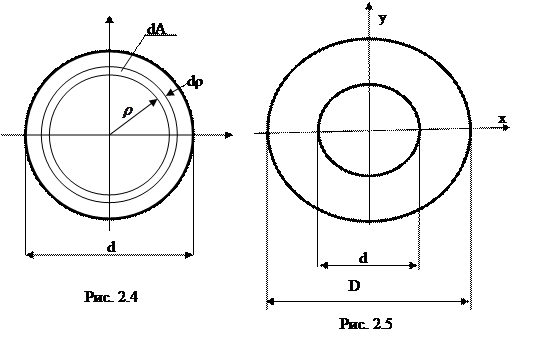
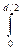 ρ2dA ═
ρ2dA ═ 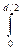 ρ22πρdρ ═
ρ22πρdρ ═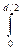 2πρ3dρ ═2πρ4 ∕ 4|
2πρ3dρ ═2πρ4 ∕ 4|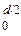 ═
═ 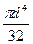
 .
.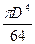 –
– 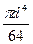 =
= 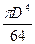 ( 1 -
( 1 - 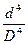 ).
).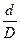 ═ α , тогда
═ α , тогда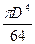 ( 1 – α4 ), І ρ=
( 1 – α4 ), І ρ=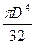 (1 – α4).
(1 – α4). 2014-02-02
2014-02-02 1143
1143








