Главные оси и главные моменты инерции сечения

Рассмотрим некоторое сечение в координатной системе x,y, а затем в координатной системе x₁,y₁, поверну-той относительно исходной на 90 ⁰ (рис.2.7). Из рисунка следует:

х₁ = у, у₁ = - х. Тогда 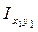= 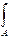х₁у₁dA ═ 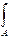-хуdA ═ - І_ху.

Таким образом, при повороте осей на 90 ⁰ центробежный момент инерции меняет знак, следовательно, есть такое положение осей, в которых центробежный момент инерции равен нулю. Такие оси называются главными. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями инерции сечения.

Моменты инерции относительно главных центральных осей называются главными центральными моментами инерции и обозначаются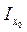,,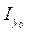причем >.

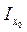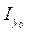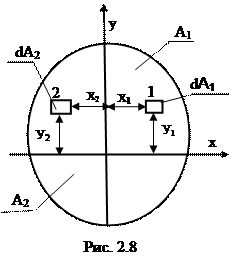
Если сечение имеет ось симметрии (ось y на рис.2.8), то эта ось всегда будет главной осью инерции сечения. Действительно, для любой элементарной площадки в окрестности точки 1 в силу симметрии найдется такая же площадка в окрестности точки 2. При этом А₁=А_2, у₁=у₂, х₁= -х_2,,тогда = + .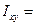

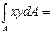
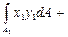
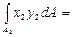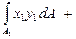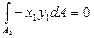Таким образом, ось у является главной осью, так как центробежный момент инерции относительно её равен нулю.