Внешнеторговые модели

Внешнеторговые модели являются разновидностью экономико-математических моделей, предназначенных для описания внешнеторговой деятельности отдельной страны или группы стран. Эти модели могут использоваться как для анализа механизмов внешней торговли (в теоретическом и прикладном плане), так и для прогнозирования внешнеторговых потоков. Теоретические внешнеторговые модели разрабатываются и используются главным образом в рамках «чистой» теории международной торговли для изучения механизмов внешнеторгового обмена на достаточно абстрактном уровне. Традиционно это модели типа 2x2x2, т. е. рассматривающие две страны, производящие два продукта (товара) с помощью двух факторов производства. В рамках этого направления сформулирован и доказан ряд теорем, ставших классическими в теории внешней торговли (теоремы Хекшера-Олина, Столпера-Самуэльсона, Рыбчинского, теорема выравнивания факторных цен).

Среди прикладных внешнеторговых моделей наибольшую популярность получили экономико-статистические модели, основанные на использовании эконометрических или балансовых методов.

Функции экспорта и импорта во внешнеторговых моделях представляются в виде уравнений регрессии и связывают величины экспорта и импорта какой-либо страны с рядом переменных как внешнего, так и внутреннего (по отношению к данной стране) характера. Данные функции можно рассматривать как производственные. Они преимущественно используются для описания крупных товарных групп, либо экспорта и импорта в целом. Функция импорта в наиболее общем виде представляется в следующем виде:

,

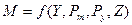где М – величина (объем) импорта;

Y – переменная, отражающая уровень экономической активности

(национальный доход, валовый национальный продукт);

Р_т и Р_y – соответственно, импортные и внутренние цены рассматриваемой

товарной группы;

Z – прочие факторы.

Вместо абсолютных значений Р_т и Р_у в приведенном уравнении иногда используют отношение 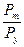, что позволяет избежать мультиколлинеарности. Это уравнение чаще всего оценивается в виде линейной логарифмической функции, поскольку в этом случае его параметры являются коэффициентами эластичности импорта по различным факторам.

Функция экспорта имеет следующую общую форму:

E = f(Y_w,P_e,P_w),

где Е – величина (объем) экспорта рассматриваемой страны;

Р_е –экспортные цены;

P_w – средневзвешенный индекс внутренних ценимпортеров;

Y_w – средневзвешенный уровень экономической активности в странах-

импортерах.

Функции экспорта и импорта могут использоваться в качестве самостоятельного инструмента экономического анализа, например:

· для выяснения зависимости между агрегированными величинами экспорта и импорта и основными макроэкономическими показателями;

· для прогнозирования величины торгового баланса;

· для расчета эластичностей экспортного и импортного спроса по ценам.

при рассмотрении внешней торговли между группой стран часто используется гравитационная модель, предназначенная для комплексного анализа двусторонних торговых потоков.

«Классическая» гравитационная модель записывается в виде уравнения:

где X_i,j – экспорт из страны i в страну j;

Y_i, Y_j – величины, характеризующие уровень экономической активности в

странах i, j соответственно (НД, ВНД);

D_i,j – расстояние между странами i, j;

а₀, а₁, а₂, а₃ – параметры модели.

Для оценки данного уравнения используется не временная (динамические ряды), а пространственная (набор стран) выборка, в основном для одного года. Оцененная гравитационная модель позволяет охарактеризовать некоторую среднюю, «нормальную» ситуацию двусторонней торговли внутри группы рассматриваемых стран.

Большое распространение в прикладных исследованиях получили матричные модели международной торговли. Если в гравитационных моделях величина двусторонних торговых потоков определяется «напрямую», то в матричных она вычисляется на основе итоговых значений объема экспорта или импорта и матрицы рыночных долей А = {а_i,j}. Отдельные элементы этой матрицы рассчитываются как отношение:

,

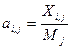где X_i,j – величина экспорта из страны i в страну j;

M_j – общий объем импорта страны j;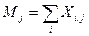

Очевидно, что при этом .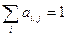

На основе матрицы рыночных долей можно записать следующие соотношения между величинами экспорта и импорта отдельных стран, а также их внешнеторговыми ценами:

,

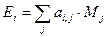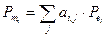
где Р_е и Р_т – соответственно экспортные и импортные цены.

Основное достоинство такой матричной записи состоит в том, что она обеспечивает балансовое равенство мирового экспорта мировому импорту, как по объему, так и по стоимости, т. е.

,

.

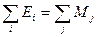Матрицу торговых долей и соответствующие ей балансовые соотношения:

,

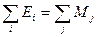можно строить как для экспорта и импорта в целом, так и для отдельных товарных групп. При использовании матричных моделей для прогнозирования международной торговли основная проблема заключается в определении будущей динамики коэффициентов а_i,j для чего разработан ряд специальных процедур.