1032
Система (2.24), по существу, состоит из двух независимых дифференциальных уравнений, содержащих неизвестные x, y, z:
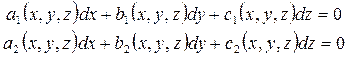(2.25)
Эти дифференциальные уравнения первого порядка носят название уравнений Пфаффа. Каждое из них дает однопараметрическое семейство поверхностей:
; 
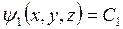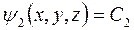(2.26)
где С1 и С2 — константы.
Линия тока должна принадлежать обеим поверхностям, т. е. она должна быть линией пересечения этих поверхностей. Очевидно, что функци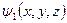и 
и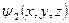 
должны быть определенным образом связаны с компонентами скорости 
, 
, 
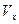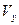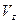. Установим эту связь.
Вектор скорости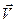 
на линии тока направлен по нормали к плоскости, образованно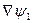й 
и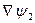 
. Поэтому можно записать
; 
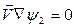(2.27)
Это означает также, что будет справедливо равенство
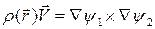(2.28)
где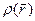 
– скалярная функция положения.
Выполнив операцию div над левой и правой частью равенства, получим
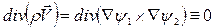
Следовательно, условие
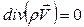(2.29)
может служить для нахождения функции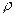 
.
Функци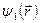и 
и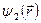 
носят название функций тока. Если 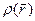известна, то векторное поле скоростей 
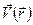может быть описано с помощью двух скалярных поле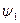й 
и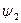 
. Вообще же функция 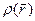подлежит определению.
В дальнейшем будет показано, что в качестве функции 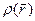выступает плотность среды. В случае несжимаемой жидкости 
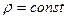и (2.29) переходит в условие несжимаемости (2.12).
Использование двух функций тока неудобно и практически не встречается. Однако в двухмерных течениях, когда скорости характеризуются только двумя компонентами, оказывается возможным рассмотрение только одной функции тока.
Рассмотрим плоское течение в плоскости Оху с компонентами скоросте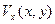й 
и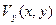 
. Тогда из (2.24)
Отсюда немедленно следует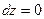 
и 
. Теперь пусть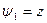 
, 
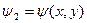. Обратимся к (2.33)
.
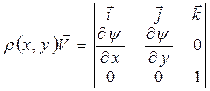Следовательно,
; 
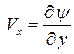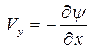(2.30)
И должно выполняться условие:
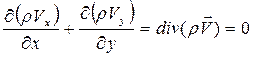(2.31)
Перейдем к описанию осесимметричных течений в цилиндрической системе координат:
, 
,
, 
.
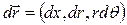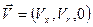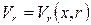На основании (2.24)
Отсюда следует
, 
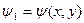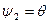
и далее
.
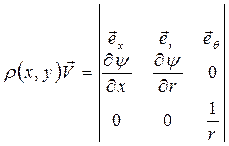Поэтому
, 
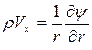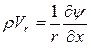. (2.32)
Должно выполняться условие
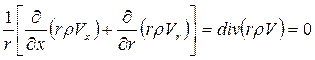. (2.33)
Функцию тока для плоского течения часто называют функцией тока Лагранжа, а для осесимметричного случая – функцией тока Стокса.
