Методы решения.
Наиболее эффективным длительное время был метод функций комплексного переменного, позволяющий получать точные аналитические решения. Однако он применим лишь для двухмерных задач, а в сложных случаях, в конечном счете, приводит к необходимости численного решения функциональных (интегральных) уравнений.
В пространственном случае наиболее общим является метод разделения переменных. Его мы рассмотрим далее более подробно. Неразрывно с ним связан метод линейных интегральных уравнений благодаря теореме эквивалентности: решению каждой краевой задачи указанного типа эквивалентно решение соответствующего интегрального уравнения.
Далее можно указать методы интегральных преобразований (Фурье, Лапласа), вариационные методы.
Принципиально новые возможности открылись у гидромехаников с развитием ПК. В настоящее время наиболее значительную группу методов составляют численные методы, которые базируются или на упомянутых ранее, или на функциях дискретного элемента (конечно-разностные методы, конечно-элементные методы). В то же время для оценки предельных свойств решений сохраняют важность различные методы возмущений и, в частности, метод асимптотических разложений.
На основании принципа относительности Галилея задачу стационарного движения тела в жидкости можно заменить задачей обтекания тела потоком, набегающим со скоростью 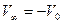 . В общем случае
. В общем случае
 (2.46)
(2.46)
Нетрудно выразить эту скорость через потенциал скорости:
 (2.47)
(2.47)
Как видим, этот потенциал удовлетворяет уравнению Лапласа, поскольку он является линейной функцией координат, а уравнение Лапласа имеет второй порядок. Суммарный потенциал скорости обозначим через 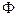 и запишем
и запишем
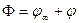 (2.48)
(2.48)
Полезно установить связь между функцией тока и скоростью невозмущенного набегающего потока в осесимметричных течениях. Учитывая связь
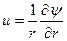 ,
,
получим
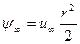 .
.
 2014-02-02
2014-02-02 589
589








