Как уже было указано, признаком потенциальности течения служит отсутствие завихренности 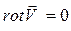 .
.
Далее введем в рассмотрение потенциал скорости 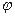 согласно зависимости
согласно зависимости
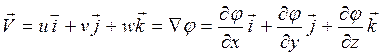 (2.39)
(2.39)
где u=Vx, v=Vy, w=Vz.
Для решения кинематической задачи, т. е. нахождения φ, имеем уравнение
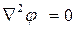 (2.40)
(2.40)
с граничными условиями:
а) на поверхности тела 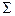
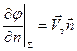 (2.41)
(2.41)
б) на бесконечности
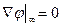 (2.42)
(2.42)
Понятие потенциала скорости введено в механику Даламбером. Уравнение (2.40) получило имя Лапласа, который вывел его в полярных координатах и исследовал многие его свойства.
Запишем уравнение Лапласа в различных системах координат:
а) в декартовой
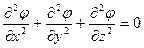 (2.43)
(2.43)
б) в цилиндрической
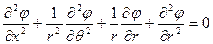 (2.44)
(2.44)
в) в сферической
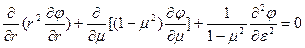 (2.45)
(2.45)
В последнем случае 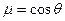 .
.
Здесь взяты лишь некоторые наиболее употребительные системы координат. Вообще же их значительно больше: полярные, биполярные, эллиптические, параболические, ортогональные, криволинейные и др. Указанные формы уравнения Лапласа помогут выявить наиболее характерные пути решения краевой задачи (2.40).. (2.42) и отметить основные свойства потенциала скоростей φ.
 2014-02-02
2014-02-02 547
547








