Пусть начало связанной системы координат движется относительно неподвижной системы Oxgygzg с поступательной скоростью 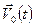 , а оси х, у, z вращаются с угловой скоростью
, а оси х, у, z вращаются с угловой скоростью 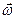 . Выразим скорость и ускорение жидкой частицы в этой системе.
. Выразим скорость и ускорение жидкой частицы в этой системе.
Если 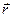 есть радиус-вектор жидкой частицы в связанной системе, то в лагранжевой формулировке скорость жидкой частицы равна
есть радиус-вектор жидкой частицы в связанной системе, то в лагранжевой формулировке скорость жидкой частицы равна
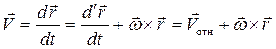 , (2.13)
, (2.13)
где 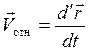 – относительная скорость движения жидкой частицы в подвижной системе, оси которой параллельны осям неподвижной системы.
– относительная скорость движения жидкой частицы в подвижной системе, оси которой параллельны осям неподвижной системы.
Абсолютная скорость 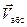 жидкой частицы в неподвижной системе, очевидно, будет равна:
жидкой частицы в неподвижной системе, очевидно, будет равна:
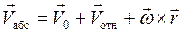 , (2.14)
, (2.14)
а переносная
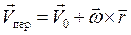 , (2.15)
, (2.15)
Определим теперь ускорение жидкой частицы:
 (2.16)
(2.16)
Раскроем значение второго члена с использованием равенства (2.13):
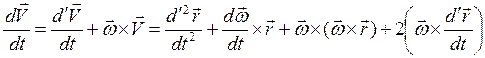 . (2.17) Здесь первый член представляет собой относительное ускорение
. (2.17) Здесь первый член представляет собой относительное ускорение
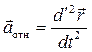 . (2.18)
. (2.18)
Переносное ускорение будет равно
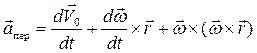 (2.19)
(2.19)
Здесь 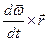 – тангенциальное ускорение,
– тангенциальное ускорение,  – центростремительное ускорение.
– центростремительное ускорение.
Последний член в (2.17) носит название Кориолисова или поворотного ускорения:
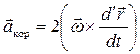 .
.
Обобщенно можно записать так:
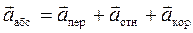 . (2.20)
. (2.20)
 2014-02-02
2014-02-02 748
748








