Введем в рассмотрение вектор вихря скорости
 |
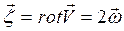 , (2.34)
, (2.34) Рис. 2.3 Вихревая линия.
называемый иногда вектором завихренности. Линии в потоке жидкости, в каждой точке которых вектор вихря скорости является касательным к данной линии, называются вихревыми линиями (рис. 2.3). Обобщение данного понятия на поверхность (вектор вихря в каждой точке поверхности должен лежать в касательной плоскости) дает понятие вихревой поверхности, или вихревого слоя (рис. 2.4). Совокупность вихревых линий, проведенных через замкнутый контур, образует вихревую поверхность, а жидкость, заключенная внутри вихревой поверхности – вихревую трубку, (рис. 2.5).
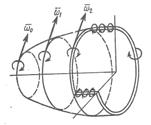 |
Рис.2.4 Вихревая поверхность.
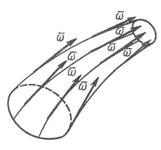 Рис.2.5 Вихревая трубка Рис.2.5 Вихревая трубка |
Теорема Гельмгольца гласит: поток вектора вихря скорости сквозь произвольно проведенное сечение вихревой трубки (или интенсивность вихревой трубки) одинаков в данный момент времени вдоль всей трубки.
Если сечения S1 и S2 выбрать достаточно малыми, чтобы их можно было считать перпендикулярными вектору, то достигается более простая формулировка теоремы.
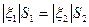 (2.35)
(2.35)
Отсюда следует важнейшее следствие: сечение вихревой трубки не может обратиться в нуль, так как это приведет к бесконечному значению завихренности (угловой скорости). Иными словами, вихревые трубки не могут заканчиваться внутри жидкости. Они могут образовывать замкнутые кривые или опираться на границы жидкой области (границы раздела).
Если вихревая трубка имеет бесконечно малое сечение, то она называется элементарной или вихревой нитью.
Интенсивность вихревой трубки удобнее выразить через циркуляцию скорости Г. В общем случае Г определяется как
Г=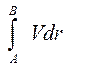 (2.36)
(2.36)
где dr — дифференциал радиус-вектора перемещения вдоль произвольного контура L, соединяющего точки А и В.
Если контур L замкнут, то
Г=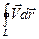
По теореме Стокса:
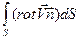 =
=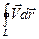
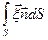 =Г, (2.37)
=Г, (2.37)
т. е. интенсивность вихревой трубки равна циркуляции скорости по замкнутому контуру, расположенному на поверхности трубки и один раз ее опоясывающему. В отечественной литературе указанный результат обычно называют теоремой Стокса.
Замкнутая вихревая нить может быть представлена в виде вихревого кольца. Совокупность вихревых нитей или вихревых колец может образовывать вихревую поверхность или вихревую пелену.
Кинематическая теорема Кельвина: индивидуальная производная по времени от циркуляции скорости по замкнутому жидкому контуру равна циркуляции ускорения по тому же контуру:
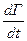 =
=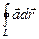 (2.38)
(2.38)
 2014-02-02
2014-02-02 1075
1075








