Общее уравнение баланса

Для анализа сложных процессов, происходящих в движущейся сплошной среде, широко используется принцип баланса (или со­хранения). Для того чтобы сформулировать этот принцип, выделим малый, но конечный объем пространства 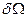, который можно на­звать контрольным. Пусть А обозначает некоторую гидродинами­ческую характеристику, например, плотность, количество движе­ния, концентрацию посторонних примесей, завихренность и т. д. Величина 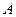может быть либо векторной, либо скалярной, либо матричной.

Согласно принципу баланса, можно утверждать: изменение величины 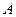за единицу времени в контрольном объеме 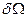может происходить за счет ее притока через поверхность 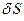,ограничива­ющую объем 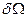, за счет генерирования (уничтожения) рассматриваемой величины внутри объема, за счет передачи этой величины внутрь объема на границах области путем различных физиче­ских процессов, например за счет молекулярного переноса. В интег­ральной форме сформулированный принцип можно записать так:

(2.53)

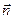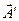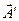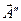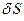Здесь – внешняя нормаль к поверхности рассматриваемого объема. Поэтому втеканию соответствует знак минус, означает мощность (обильность) источников (или стоков) рассматриваемой величины. Иными словами, означает объемный расход величины , генерируемый источниками (стоками); означает расход вели­чины через поверхность , обусловленный различными физиче­скими процессами. Пусть, например, 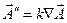. Тогда последнее слагаемое будет описывать процессы диффузии или теплопередачи.

В правой части (2.53) могут содержаться и другие слагаемые, обусловленные физическими процессами различной природы.

С помощью теоремы Гаусса-Остроградского можно перейти от поверхностных интегралов к объемным. Тогда получим уравнение баланса в дивергентной (или консервативной) форме:

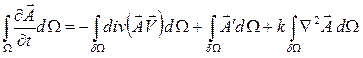(2.54)

Если источники отсутствуют, т.е. 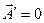, и нет молекулярного переноса 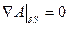, то

(2.55)

Это означает, что изменение какой-либо характеристики жидкой среды происходит только за счет переноса, обусловленного ее дви­жением. Поэтому уравнение (2.55) можно назвать уравнением переноса в жидкой среде. В покоящейся жидкой среде

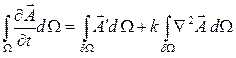(2.56)

Отсюда следует, что изменение какой-либо характеристики жид­кой среды может происходить вследствие действия источников (стоков) и процессов, диффузии.

Если подынтегральные выражения в (2.54) существуют и непрерывны в каждой точке рассматриваемого объема, то можно перейти от интегральной формулировки принципа баланса к дифференциальной:

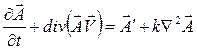(2.57)

Необходимо подчеркнуть принципиальную разницу между интегральной и дифференциальной формулировками. В первом случае допустимы течения жидкости со скачкообразными изменениями параметров. Дифференциальные же формулировки таких возмож­ностей не позволяют. Как будет показано в дальнейшем, реальные течения могут содержать поверхности разрыва нормальной или тангенциальной скорости, скачкообразного изменения плотно­сти и давления. Поэтому зачастую интегральные формулировки предпочтительны.

Существует и другой аспект преимущества интегрального под­хода к изучению движения жидкой среды. Если течение стационарно и источники отсутствуют, то справедливо соотношение

(2.58)

Иными словами, течение жидкости полностью определяется процессами, разыгрывающимися только на поверхности, ограничи­вающей объем жидкости.

Принцип баланса позволяет сформулировать основные законы сохранения, которым подчиняется движущаяся жидкая среда, а именно: законы сохранения массы, количества движения, энергии.