Пусть уравнение свободной поверхности задается в неявном виде S(x, у, z, t)=0. Тогда кинематическое условие устанавливает, что
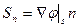 , (2.49)
, (2.49)
т. е. нормальная составляющая скорости свободной поверхности равна нормальной составляющей жидкой частицы, лежащей на свободной поверхности. Иными словами, кинематическое условие также является, по существу, условием непротекания. Придадим этому условию более компактный вид. Для этого выразим скорость Sn
Рассмотрим уравнение поверхности S в момент времени t+dt:
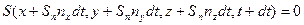 ,
,
где nx, ny, nz -направляющие косинусы единичной нормали ксвободной поверхности.
Дифференцирование этой функции по времени даст
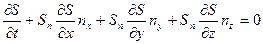
Отсюда
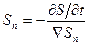
Теперь кинематическое условие может быть переписано в форме

или
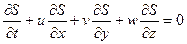 (2.50)
(2.50)
Но полученное выражение есть не что иное, как полная производная S по времени, т. е.
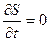 (2.51)
(2.51)
Таким образом, получен искомый вид кинематического условия на свободной поверхности. Очень часто уравнение свободной поверхности задается уравнением
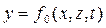
Тогда кинематическое условие приобретает вид
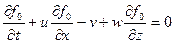 (2.52)
(2.52)
 2014-02-02
2014-02-02 552
552








